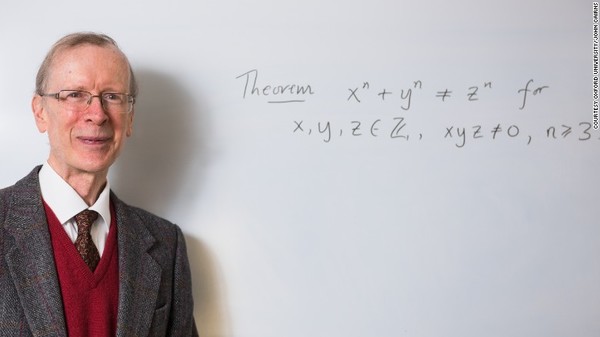数学家怀尔斯《数学与文化》相关文章:数学和数学家的故事

2017-10-23

字体:

大中小

浏览:

文章简介：要问在历史上这些数学家中我最佩服谁,那肯定是欧拉.欧拉小学就被开除了,因为他问的问题太多,给老师太多的难堪.有人说欧拉是先会算术后会说话的,高斯也是这样,高斯一岁时就能发现父亲账本上计算的错误,不过这肯定是传说.但是欧拉很小就知道等周原理:在周长固定的所有图形,面积最大的一定是圆.大名鼎鼎的约翰.贝努力是欧拉父亲的朋友,第一次见到六岁的欧拉就被欧拉问住了:"我知道一个数6,它有因数1,2,3,6,加起来是6的2倍;还有一个数28,有因数1,2,4,7,14,28,加起来也是28的2倍,还有多少这

要问在历史上这些数学家中我最佩服谁,那肯定是欧拉。

欧拉小学就被开除了,因为他问的问题太多,给老师太多的难堪。有人说欧拉是先会算术后会说话的,高斯也是这样,高斯一岁时就能发现父亲账本上计算的错误,不过这肯定是传说。但是欧拉很小就知道等周原理:在周长固定的所有图形,面积最大的一定是圆。

大名鼎鼎的约翰。贝努力是欧拉父亲的朋友,第一次见到六岁的欧拉就被欧拉问住了:"我知道一个数6,它有因数1,2,3,6,加起来是6的2倍;还有一个数28,有因数1,2,4,7,14,28,加起来也是28的2倍,还有多少这样的数?"这类数叫做完全数,还是欧拉,最终给出了偶数完全数的表达式,那是后来的事情了。

对于奇数的情形,谁要是能正确证明有或者没有,现在肯定能拿到数学最高奖。欧拉17岁获得了瑞士巴赛尔大学的硕士学位,欧拉太专注数学,以至于贝努力不得不规定,吃饭时间不许看书。他19岁时被俄罗斯卡德琳娜女王邀请到彼得堡科学院从事研究。

欧拉解决的问题实在太多了,解决问题过程中创造出的方法不知开创了多少个数学分支。欧拉因为解决着名的七桥问题开创了拓扑学,歌德巴赫猜想是因为歌德巴赫和欧拉的通信而出名的。任何一个正整数都一定能写成不超过四个平方数之和是欧拉最早证明的,这可是将近两千年无人解决的问题。

数论,几何,力学,天体力学,到处留下欧拉的足迹。现代数学的符号和表达式,如三角,指数,e,i,π等等,都是欧拉创立的。历史上第一本流行的微积分教科书也是欧拉写的。后来所有的微积分教科书,或者是抄袭欧拉的,或者是抄袭抄袭欧拉的。

欧拉研究数学,就像人在呼吸,鸟在飞翔一样自由和自在。

欧拉早就发现了‘变分法’可是当他发现法国人拉格朗日也有这类思想时,就把自己的藏起来不发表,把出名的机会留给年轻人。

欧拉由于看书过多,年轻时就瞎了一只眼睛,到59岁时,他的左眼也逐渐失明了。正当他抢在完全失明前抢救资料时,一场大火烧毁了他的一切资料。

欧拉大部分工作是在失明以后完成的,包括四平方定理。

欧拉的两个学生因为计算一个无穷级数答案不一样发生争执,失明的欧拉用心算找出了小数点后第50位的错误,结果证明这两个学生都算错了。这就是欧拉。

五、业余高手(1)

在当今日益专业话的分工下,无论是竞技项目还是专业领域,业余爱好者也许永远达不到专业人员的水平。就拿围棋为例,每年中国的专业vs业余最高对抗赛,尽管专业棋手让两个子,可是业余棋手还是几乎全军覆没,象棋领域也大概如此。不过韩国围棋高手刘昌赫曾经是业余棋手,但最后达到了专业超一流棋手的水平。象棋全国冠军陶汉明曾经是业余棋手起家,曾经取得过全国亚军的金波也是业余棋手。不过这些只是极端个别的例子。

在数学发展起步时期,业余数学家取得了骄人的成绩。依我看,费尔马(Femart)应该是自古以来没有与之相比的,估计今后也不会有超越他的业余数学家了。费马(1601年~1665年)是一位具有传奇色彩的业余数学家,他最初学习法律并以当律师谋生,后来成为议会议员,数学只不过是他的业余爱好,只能利用闲暇来研究。

虽然年近30才认真注意数学,但费马对数论和微积分做出了第一流的贡献。费马提出了光线沿最快的路径行进的原理,进而揭示了隐藏在光的折射定律后面的自然界的秘密,原来只有服从折射定律,才能保证光线从一点到达另一点用的时间最短。

费马在数论上为我们留下了大量的定理和猜想,其中相当一部分未给出证明。挑选这些‘定理’中最有趣的两个给大家介绍一下。

费尔马猜测,形如2^(2^n) 1(这里符号‘^’表示幂,如4^2=16)的数都是素数,这类数成为费尔马数。对于n=0,1,2,3,4,经过验证果然如此。不过对于n=5,欧拉用心算得出:2^(2^5) 1=2^32 1=641×6700417,不是素数。有趣的对于其它的n,至今没发现一个费尔马数是素数。

下面说说着名的‘费马大定理’:那是费马去世后,人们整理他留下的笔记发现的。费马热衷于不定方程的研究。我想能够坚持读本文的读者应该都知道勾股定理,并知道3^2 4^2=5^2,5^2 12^2=13^2,等等,这类数叫做勾股数(国际上叫毕达哥拉斯数),这类数究竟是怎样构造出来的,古希腊时期已经给出了完整的答案:如果x是偶数,且x和y没有公因数,那么必然有有一奇一偶两个正整数a,b,使得:x=2ab,y=a^2-b^2,z=a^2 b^2,其中a和b没有公因数。

费尔马在阅读一本书叫做【丢番图方程】里面关于勾股数这部分时,在旁边写到:把一个整数的立方写成两个整数的立方之和,把一个整数的四次方写成两个整数的四次方之和,等等,都是不可能的。我已经找到了绝妙的证明,可惜这本数旁边的空白处太少了,我写不下来。

费尔马这个没有写下来的证明,天晓得到底存在还是不存在,可是他的这段话是坑了不少人。欧拉和高斯试图证明这个定理,最后都失败了。一战之前,曾经有个德国人悬赏十万马克给第一个证明费尔马大定理的人,一时许多业余高手都投入到这场奖金的争夺中,但是没有一个证明是正确的。

一战以后,德国马克贬值,这笔奖金化作一堆废纸。有人问大数学家希尔伯特(Hilbert)为什么不试试证明这个定理,他说:"这是只下金蛋的鹅,我为什么要杀掉它呢?"(意思是说这个定理能引诱好多人从事数学研究,不证明它更好。)

这个定理折磨了数学家整整三百年,直到1993年,一个叫怀尔斯的数学家用难以置信的方法给出了证明。1980年怀尔斯在剑桥大学取得博士学位后来到了美国普林斯顿大学,并成为这所大学的教授。从1986年开始,这家伙七年时间没有发表任何论文,要是在中国他什么经费和津贴都别指望了。

1993年6月23日,牛顿研究所举行了20世纪最重要的一次数学讲座。两百名数学家聆听了这一演讲,但他们之中只有四分之一的人完全懂得黑板上的希腊字母和代数式所表达的意思。

演讲者就是是安德鲁·怀尔斯。怀尔斯回忆起演讲最后时刻的情景:"虽然新闻界已经刮起有关演讲的风声,很幸运他们没有来听演讲。但是听众中有人拍摄了演讲结束时的镜头,研究所所长肯定事先就准备了一瓶香槟酒。

当我宣读证明时,会场上保持着特别庄重的寂静,当我写完费马大定理的证明时,我说:‘我想我就在这里结束’,会场上爆发出一阵持久的鼓掌声。

"因为他证明了这个大定理。不过说点题外的话,后来又发现他的证明有漏洞,又折磨了他一段时间,到1994年9月,他把所有的漏洞都堵上了。这个证明后来经过精练,已经缩短到130多页,最初的证明有400多页。怀尔斯一下子成了传媒的宠儿和明星,这是数学家少有的抛头露脸的机会,大概是费尔马大定理的内容通俗易懂而证明却持续了300多年吧。

怀尔斯的故事告诉我们:中国目前高校搞急功近利的唯文章数量评价水平的作法,肯定不会出现重大的研究成果。

六、业余高手(b)

提起业余数学家或者数学研究者,每次都使我肃然起敬。在中国,出于对数学中歌德巴赫猜想的兴趣而爱好数学的有一大批人,笔者有幸在互联网和生活中遇见到其中的几个。记得以前看到电视节目【东方时空】百姓故事栏目例介绍了一个业余研究歌德巴赫猜想的一位老先生,自己靠蒸馒头卖钱度日,却把大部分收入用在了歌德巴赫猜想上。

虽然研究数学不用什么花销,可是购买资料请教问题要外出吧,要有路费和旅途上的费用吧。这些研究歌德巴赫猜想的人有共同的特点,几乎都宣称自己证明出来了,可是却无法发表在公开出版的学术刊物上,或者被别人挑出错误可是自己还不能理解。

在一些论坛上,经常看到有关歌德巴赫猜想的证明,有的看起来还很巧妙。比如我看到一个证明就用到了集合论中很深奥的‘良序公理’,这个公理和‘选择公理’等价。

他巧妙的构造一系列集合,可惜他错误的理解了良序公理中‘任何集合都能被良序’,而一厢情愿的认为良序就是一类集合的包含。

这些人抱着‘一夜成名’的心态的毕竟是少数,多数是出于对数学的热爱,却由于各种原因,没有机会走上专职研究数学的道路。

德国数学家外尔斯特拉斯(Weierstrass:1815--1897)也算业余高手,后来走上了职业数学家的道路。他开始是学习法律和财经,一度在在中学任教。这大概是中学数学教师中最杰出的一位了。德国是一个多出哲学家的国度,德国人又以严格认真见长,外尔斯特拉斯也是一样,他的品性最能体现德国人对待真理的态度了。他最大的贡献是在微积分严格化上作出了杰出的贡献。

微积分在创立初期,理论上还不够严密性,无穷小变成了神秘和随心所欲被理解的量。因此1734年,英国哲学家、大主教贝克莱发表了文章《向一个不信神的数学家的进言》,矛头指向微积分的基础--无穷小的问题,提出了所谓贝克莱悖论。

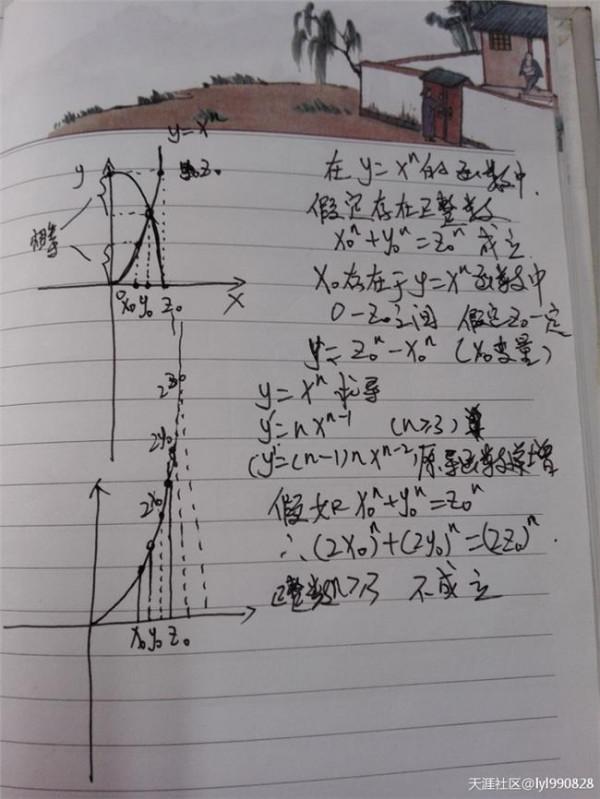
他指出:"牛顿在求x^n的导数时,采取了先给x以增量0,应用二项式(x 0)^n,从中减去x^n以求得增量,并除以0以求出x^n的增量与x的增量之比,然后又让0消逝,这样得出增量的最终比。

这里牛顿做了违反矛盾律的手续──先设x有增量,又令增量为零,也即假设x没有增量。"他认为无穷小dx既等于零又不等于零,召之即来,挥之即去,这是荒谬,)"是消失了的量的鬼魂。。。。。。能消化得了二阶、三阶流数的人,是不会因吞食了神学论点就呕吐的。"无穷小量究竟是不是零?无穷小及其分析是否合理?由此而引起了数学界甚至哲学界长达一个半世纪的争论。导致了数学史上的第二次数学危机。

外尔斯特拉斯和法国的一些数学家一道,使得微积分无懈可击。

外耳斯特拉斯还告诉我们,直观有时是靠不住甚至是完全错误的。从前人们直观上一直认为连续曲线肯定是光滑的,或者大多数点都是光滑的。用在函数上,就是一直认为连续函数是可导的,或者在多数点是可导的。可是外尔斯特拉斯却举出一个反例,在每一个点都连续,却有在任何点都不可导。他举出这个函数是画不出图像的,当时作为一个中学教师,的确令数学家们大跌了眼镜。

1851年,大数学家高斯最得意的弟子黎曼,在博士论文中提出了一个原理:狄利赫来(Dirichlet)原理,利用这个‘原理’,可以美妙的解决变分中提出的一系列问题,并且在数学物理上有着广泛的应用。

按照微积分理论,狄利赫来原理应该算是理所当然成立的。可是外尔斯特拉斯却说:"不加证明的使用狄利赫来原理,是不严格的。"黎曼也是很谦虚的,便回应到:"您说的对,不过这个原理肯定是正确的,很快我就会证明出来。

"但是黎曼直到去世也没有证明出来,又是这个中学教师,举出了一个反例,彻底推翻了狄利赫来原理。于是黎曼博士论文中的一切结果都是值得怀疑的了。因此数学家卡尔。诺依曼叹息道:"如此美妙而又有广泛应用前景的原理,已经永远从我们视野中消失了。"

1899年,旷世奇才希尔伯特(Hilbert)用了不到6页纸,通过附加一个条件,就消除了黎曼理论的缺陷,从而挽救了这个原理。更神奇的是,还挽救了黎曼的名声,因为用这个改造的原理发现黎曼所得的其它结果又都是正确的了。

这真是群星闪耀的年代,是数学家自由飞翔的年代。可惜一去不复返了。

七、天妒英才

下面要说到两个英年早逝的数学家,伽罗瓦和阿贝尔,不过要先从一个故事说起。

凡是受过初中教育的人都知道,任何一个一元二次方程都可以用求根公式求出它的解,这大概是很久就有的公式了。其中根和系数的关系被称作韦达定理,有着广泛的应用。然而三次方程和四次方程甚至更高阶方程的求解公式一直不被人们所知。在文艺复兴时期,有个叫塔塔利亚的业余数学家首先得到了这个公式,不过他秘而不宣,这是当时搞研究的人的一个传统。可是,这个消息还是在寻求公式的一些业余数学家之间流传着。

有一个叫卡当的业余研究者找到了塔塔利亚,恳求得到塔塔利亚的真传。这个卡当在赌博上也不是一般的赌徒,是他在赌博中提出了概率的思想,他还热衷于炼金术,星象学。塔塔利亚肯定被卡当打动了,也许卡当常跪不起,也许甜言蜜语,总之塔塔利亚告诉了他自己知道的一些公式。

卡当学到手求解公式后就离开了塔塔利亚,甚至把对塔塔利亚许下的诺言抛到了九霄云外,写出了一本术,名字叫做‘大术’,介绍了三次方程四次方程的求解方法。于是卡当声名雀起,因为他在书中宣称这些公式是他自己发现的。

两个人的争执开始了,解决争端的方法很简单,来一场决斗:两人各自给对方出20道题,看谁先解出来。塔塔利亚大获全胜,卡当一道题都没有解出来,因为塔塔利亚教他时留了一招,没有把公式的一般情况告诉卡当。这大概是人类历史上的第一场数学竞赛,参赛这只有两个人,这个故事发生在四百多年前。

不过至今这些公式还被称作卡当公式,而塔塔利亚连名字都没有留下来,塔塔利亚只是一个外号,意大利语意思是‘结结巴巴的人’的意思。

历史就像一条河流,沉到河里的往往是金子,浮在河面上的往往是水草和马粪。

三次四次方程求根公式得到了以后,人们寻求五次和五次以上方程的求解公式。可是欧拉高斯等杰出数学家都没有找到求解公式,成了当时数学的难题。有两个青年匆匆的来到了这个世界,又匆匆的离开了,也许他们来到人世的目的就是为了给我们一些惊讶和慨叹。

尼尔斯·亨利克·阿贝尔(N。H。Abel)1802年8月5日出生在挪威一个名叫芬德的小村庄。阿贝尔幸运的碰到了一个有数学头脑却无多大数学成果的老师,老师很快发现他的数学才能,使得他很早就接触到了微积分。

在中学的最后一年,阿贝尔开始试图解决困扰了数学界几百年的五次方程问题。在19岁那年,他证明了一般五次方程求解公式不存在,就是说,不能用方程系数和开根号的有限多次运算来表示方程的根。

阿贝尔认为这结果很重要,便自掏腰包在当地的印刷馆印刷他的论文。因为贫穷,为了减少印刷费,他把结果紧缩成只有六页的小册子。阿贝尔满怀信心地把这小册子寄给国内外的一些数学家,包括数学王子的高斯,希望能得到一些反应。

可惜他的文章太简洁了,没有人能看懂。高斯收到这小册子时觉得不可能用这么短的篇幅证明这个世界着名的问题―――连他还没法子解决的问题。他看都没看一眼,就把它扔在书堆里了。阿贝尔的另一篇论文是他在欧洲旅行时通过别人转交给大数学家柯西(Cauchy)手里,柯西连看都没看就扔到纸篓里。

阿贝尔饥寒交迫的回到了挪威,还欠了一身债,最后在绝望中死去,年仅27岁。他活着最大的理想是在大学里当一个讲师,可是到死都没有实现。看看现在大学里教授成堆,博士成群,可是这个群体再也没有疯疯癫癫的学者,没有目光深邃的思想者,没有疯狂的怪癖人物了。

伽罗瓦(EvaristeGalois)1811年10月25日生于巴黎附近的一个小城。1829年他两次投考巴黎综合工科学校,却因思想激进,两次被拒绝录取,最后只好进入高等师范学校学习。1829年5月,17岁的他写出了关于五次方程的代数解法的论文,论文中首次引入"群"的概念。

他把论文寄给经由柯西,请他交给法兰西科学院审查。柯西对此根本不屑一顾,把这个中学生的文章给弄丢了。1830年2月伽罗瓦再次将他的研究成果写成一篇详细的论文,寄给科学院秘书傅立叶,不料当年5月傅立叶病死,伽罗瓦的文稿再次被丢失。

1831年伽罗瓦第三次将论文送交法国科学院。泊松院士看了4个月,最后在论文上批道:"完全无法理解"。可惜这些大数学家的傲慢和自大,使得伽罗瓦的理论被埋没了将近50年。

伽罗瓦因为政治激进,被阴谋的政客们用一件小事怂恿和一个军官决斗。在决斗前一个晚上,他急切地写着他的遗言。想在死亡来临之前尽快把他的思想中那些有意义的东西写出来。他不时中断,在纸边空白处写上"我没有时间,我没有时间。"接着伽罗瓦又写下一个潦草的大纲。他在天亮之前那最后几个小时写出的东西,一劳永逸地给一个折磨了数学家几个世纪的难题题找到了真正的答案,开创了数学上的一个重要的分支―――群论。