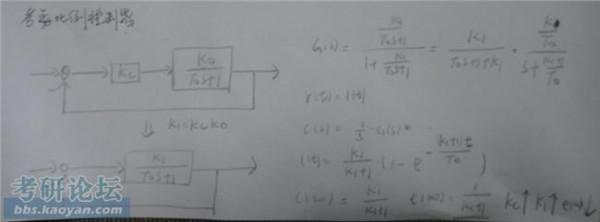
初学数学分析 吉米多维奇的很多证明题都做不懂 是正常情况吗?

2017-11-07
字体:
大中小
浏览:
文章简介：具体到题主你的这个问题,只能说明你对数学分析里面的基本技巧掌握得不熟.这个极限问题即便不用Taylor公式,也可以从数e的定义出发比较轻松地解决.这种时候不论做什么样的计算型证明习题对于你掌握基本技巧都是有好处的.但是当你能够熟练解决这类问题的时候,吉米多维奇就不够用了.吉米多维奇中的重复问题非常非常之多,而证明题占的比例其实很小.只做吉米多维奇的确可以磨练计算能力,但对逻辑思维能力基本上不会有任何帮助.我举一个常常让初学者纠结的证明:证明3倍根号2等于根号18. 实际上这个证明严重地依赖于你对

具体到题主你的这个问题,只能说明你对数学分析里面的基本技巧掌握得不熟。这个极限问题即便不用Taylor公式,也可以从数e的定义出发比较轻松地解决。这种时候不论做什么样的计算型证明习题对于你掌握基本技巧都是有好处的。

但是当你能够熟练解决这类问题的时候,吉米多维奇就不够用了。吉米多维奇中的重复问题非常非常之多,而证明题占的比例其实很小。只做吉米多维奇的确可以磨练计算能力,但对逻辑思维能力基本上不会有任何帮助。

我举一个常常让初学者纠结的证明:证明3倍根号2等于根号18. 实际上这个证明严重地依赖于你对实数定义方式的选择。如果你默认了乘幂的存在性然后证明它的乘法性质,那么这个问题很容易解决。然而我们不知道吉米多维奇到底采取哪种定义。

难道把所有的可能证明都写出来吗?初学者常常为此纠结,可是实际上全无必要。太过注重这种细节,在以后学分析的时候容易把握不了全局。 我个人比较推荐的书是菲赫金哥尔兹的微积分学教程(练计算,多见些例子)。

至于原理性的东西,这种老教材的讲法往往很绕也很繁琐。这时候推荐卓里奇或者Rudin. 顺便补一句,不让用Taylor公式太流氓了。以后碰上实际问题的时候,这种级别的极限问题还去做什么不等式放缩?什么办法好用就用什么办法。