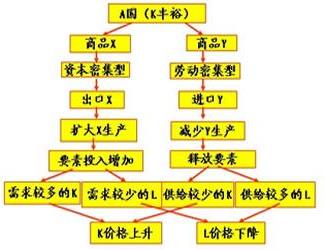
柯布-道格拉斯生产函数三者关系深化探讨

    辽宁工程技术大学        数学建模课程成绩评表    学专期08-09学年1学期姓业机械电子工程班名级刘友海机电06-1        课程名称论文题目        数学建模柯布-道格拉斯生产函数柯布道格拉斯生产函数评定指标    知识创新性理论正确性内容难易性        分值    20201510151010100        得分        评定标准评语:评语        结合实际性知识掌握程度书写规范性工作量总成绩        任课教师李付举        时        间        08年11月25日        备        注        数学建模        柯布-道格拉斯生产函数柯布道格拉斯生产函数    摘要:柯布-道格拉斯生产函数是用来预测国家和地区的工业系统或大企业的生产和分析发展生产的途径的一种经济数学模型。

根据对国民生产总值、固定资产和劳动力关系的了解,以及相关数据的表格统计,运用数学建模的相关知识建立相关柯布-道格拉斯生产函数模型。本文讲从农业、经济、柯布-道格拉斯生产函数三者关系深化探讨,进一步分析未来三者对社会经济及发展的影响。

关键字:柯布-道格拉斯生产函数;农业;经济        一、模型简述    柯布-道格拉斯生产函数基本的形式为:式中Y是工业总产值,A是综合技术水平,L是投入的劳动力数(单位是万人或人),K是投入的资本,一般指固定资产净值(单位是亿元或万元,但必须与劳动力数的单位相对应,如劳动力用万人作单位,固定资产净值就用亿元作单位),是劳动力产出的弹性系数,β是资本产出的弹性系数,?表示随机干扰的影响,?≤1。

从这个模型看出,决定工业系统发展水平的主要因素是投入的劳动力数、固定资产和综合技术水平(包括经营管理水平、劳动力素质、引进先进技术等)。根据和β的组合情况,它有三种类型:①+β1,称为递增报酬型,表明按现有技术用扩大生产规模来增加产出是有利的。②+β1,称为递减报酬型,表明按现有技术用扩大生产规模来增加产出是得不偿失的。

③+β=1,称为不变报酬型,表明生产效率并不会随着生产规模的扩大而提高,只有提高技术水平,才会提高经济效益。美国经济学家R.M.斯诺提出的中性技术模式即斯诺模型属于不变报酬型。当?=1时,斯诺模型为:        或        式中(1-)是劳动力产出的弹性系数。

根据弹性系        数的经济意义和数学意义,        这里p是产出价格,是资本价格当=        时,        。

它表示对生产技术水平、经营管理水平和服务水平的综合评        价,全面反映企业的适应能力、竞争能力和生存能力。A()值越大,水平越高。根据柯布-道格拉斯生产函数可以得到下列经济参数(设?=1):①劳动力边际生产力表示在资产不变时增加单位劳动力所增加的产值。

②资产边际生产        力        表示在劳动力不变时增加单位资产所增加的产值。

③劳力对资产的边        1        刘友海:柯布-道格拉斯生产函数        际代换率        表示产值不变时增加单位劳动力所能减少的资产值。

④劳        动力产出弹性系数        ,表示劳动力投入的变化引起产值的变化的速率。

⑤资产产        出弹性系数        ,表示资产投入的变化引起产值变化的速率。

国际上一般取=        0.2~0.4,=0.8~0.6。中国根据国家计委测算一般可取=0.2~0.3,=0.8~0.

7。        二、问题引入    经济学中著名的柯布-道格拉斯(Cobb-Douglas)生产函数的一般形式为Q(K,L)=aKαLβ,0α,β1其中Q,K,L分别表示产值、资金、劳动力,式中α,β,a要由经济统计数据确定。

现有《中国统计年鉴2003)给出的统计数据如表(》(其中总产值取自“国内生产总值”,资金取自“固。定资产投资”,劳动力取自“就业人员”)    表年份1984198519861987198819891990199119921993199419951996199719981999200020012002总产值/万亿元0.

71710.89641.02021.19621.

49281.69091.85482.16182.66383.46344.67595.84786.78857.44637.83458.20689.94689.731510.4791经济统计数据资金/万亿元0.

09100.25430.31210.37920.47540.44100.45170.55950.80801.30721.70422.00192.29142.49412.84062.98543.

29183.73144.3500劳动力/亿人4.81794.98735.12825.27835.43345.53296.47496.54916.61526.68086.74556.80656.89506.

98207.06377.13947.20857.30257.3740        要求:1)运用适当的方法,建立产值与资金、劳动力的优化模型,并作出模型的分(    2        数学建模        析与检验。

(2)建立Cobb-Douglas优化模型,并给出模型中参数α,β的解释。(3)将几个模型作出比较与分析。        三、模型假设    用来预测国家和地区的工业系统或大企业的生产和分析发展生产的途径的一种经济数学模型,简称生产函数。

它的基本的形式为:        式中Y是工业总产值,A是综合技术水平,L是投入的劳动力数(单位是万人或人),K是投入的资本,一般指固定资产净值(单位是亿元或万元,但必须与劳动力数的单位相对应,如劳动力用万人作单位,固定资产净值就用亿元作单位)是劳动力产出的弹性系数,β,是资本产出的弹性系数,?表示随机干扰的影响,?≤1。

从这个模型看出,决定工业系统发展水平的主要因素是投入的劳动力数、固定资产和综合技术水平(包括经营管理水平、劳动力素质、引进先进技术等)。根据和β的组合情况,它有三种类型:①+β1,称为递增报酬型,表明按现有技术用扩大生产规模来增加产出是有利的。

②+β1,称为递减报酬型,表明按现有技术用扩大生产规模来增加产出是得不偿失的。③+β=1,称为不变报酬型,表明生产效率并不会随着生产规模的扩大而提高,只有提高技术水平,才会提高经济效益。美国经济学家R.

M.斯诺提出的中性技术模式即斯诺模型属于不变报酬型当?=1时,。斯诺模型为:        Y=A(t)L1?εKε或式中(1-ε)是劳动力产出的弹性系数。

根据弹性系数的经济意义和数学意义,。这里p是产出价格,q是资本价格。当p=q时,。        。它表示对生产技术水平、经营管理水平和服务水平的综合评价,全面反映企业的适应能力、竞争能力和生存能力。

A(t)值越大,水平越高。根据柯布-道格拉斯生产函数可以得到下列经济参数(设?=1):①劳动力边际生产力表示在资产不变时增加单位劳动力所增加的产值。

        ②资产边际生产力        表示在劳动力不变时增加单位资产所增加的产值。

        ③劳力对资产的边际代换率        表示产值不变时增加单位劳动力所能减    3        刘友海:柯布-道格拉斯生产函数        少的资产值。

④劳动力产出弹性系数,表示劳动力投入的变化引起产值的变化的速率。        ⑤资产产出弹性系数        ,表示资产投入的变化引起产值变化的速率。

国际上一般        取=0.2~0.4,=0.8~0.6。

中国根据国家计委测算一般可取=0.2~0.3,=0.8~0.7。        四、分析建立模型    增加生产、发展经济所依靠的主要因素有增加投资、增加劳动力以及技术革新等,在研究国民经济产值与这些因素的数量关系时,由于技术水平不像资金、劳动力那样容易定量化,作为初步的模型,可认为技术水平不变,只讨论产值和资金、劳动力之间的关系。

在科学发展不快时,如资本主义经济发展的前期,这种模型是有意义的。用Q,K,L分别表示产值、资金、劳动力,要寻求数量关系Q(K,L)。经过简化假设与分析,在经济学中,推导出一个著名的Cobb-Douglas生产函数:0α,β1Q(K,L)=aKαLβ,式中α,β,a要由经济统计数据确定。

现有《中国统计年鉴(2003)》给出的统计数据如表(其中总产值取自“国内生产总值”,资金取自“固定资产投资”,劳动力取自“就业人员”)。    表年份1984198519861987198819891990199119921993199419951996199719981999200020012002总产值/万亿元0.

71710.89641.02021.19621.

49281.69091.85482.16182.66383.46344.67595.84786.78857.44637.83458.20689.94689.731510.4791经济统计数据资金/万亿元0.

09100.25430.31210.37920.47540.44100.45170.55950.80801.30721.70422.00192.29142.49412.84062.98543.

29183.73144.3500劳动力/亿人4.81794.98735.12825.27835.43345.53296.47496.54916.61526.68086.74556.80656.89506.

98207.06377.13947.20857.30257.3740        4        数学建模        其中Q,K,L分别表示产值、资金、劳动力,式中α,β,a要由经济统计数据确定。

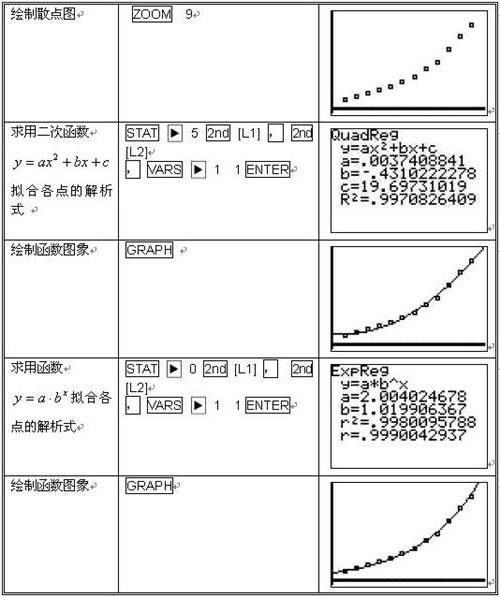
        五、求解模型    第一种方法:由于产值Q、资金K、劳动力L之间满足著名的Cobb-Douglas生产函数关系:Q(K,L)=aKαLβ,0α,β1我们可以用MATLAB软件中的curvefit()程序来作数据拟合,即寻求函数Q(K,L)中的未知参数a,α,β,使这个函数尽量逼近表1所给出的统计数据。

现在我们就根据curvefit()函数编以下程序程序文件a1.m如下a=[0.71710.89641.02021.19621.49281.69091.85482.16282.66383.46344.67595.

84786.78857.44637.83458.20689.94689.731510.4791];y=[0.09100.25430.31210.37920.47540.44100.45170.

55950.80801.30721.70422.00192.29142.49412.84062.98543.29183.73144.3500;4.81794.98735.12825.27835.43345.

53296.47496.54916.61526.68086.74556.80656.89506.98207.06377.13947.20857.30257.3740];x0=[0.1,0.1,0.2];x=curvefit(curvefun,x0,y,a)其中的函数M——文件curvefun.m如下functiona=curvefun(x,y)a=x(1)*(y(1,:).