蔡子星物理竞赛 高中物理竞赛讲义(超级完整版)

76 x 时准静态过程无法达 成(T 升高时,P 增大而 x 减小) ,水银自动溢出。 所以,自动溢出的条件是:T > 7296) 考查函数 y = 1 19.2 1 19.2 (-x2 20x (-x2 20x 7296)发现, 当 x = 10cm 时,ymax = 385.

2K 而前面求出的 x = 0 时,T 只有 380K,说明后阶段 ... 无须升温,即是自动溢出过程 (参照图 6-8 理解) 。

而 ............. T > ymax 即是题意所求。 【答案】385.2K 。 a、推论 1: P1 ?1T1 = P2 ? 2 T2 ,此结论成功地突破了“质量一定”的条件约束, 对解某些特殊问题非常有效。

b、克拉珀龙方程:原方程中,将“恒量”定量表达出来就成为 PV = ? RT , 其中 ? 为气体的摩尔数,这个结论被成为克拉珀龙方程。它的优点是能使本来针 对过程适用的方程可以应用到某个单一的状态。

c、推论 2:气体混合(或分开)时, P1V1 T1 P2 V2 T2 … Pn Vn Tn ? PV T ,这 个推论很容易由克拉珀龙方程导出。 【例题 6】图 6-9 是一种测量低温用的气体温度计,它的下端是测 温泡 A ,上端是压力计 B ,两者通过绝热毛细管相连,毛细管容积不 计。

操作时先把测温计在室温 T0 下充气至大气压 P0 ,然后加以密封, 再将 A 浸入待测液体中, 当 A 和待测液体达到热平衡后, B 的读数为 P , 已知 A 和 B 的容积分别为 VA 和 VB ,试求待测液体的温度。

【解说】本题是“推论 2”的直接应用 P0 (VA ? VB ) T0 = PVA TA PVB T0 【答案】TA = PVAT0 P0 (VA ? VB ) ? PVB 【例题 7】图 6-10 所示是一定质量理想气体状态变化所经历的 P-T 图线,该图线是以 C 点为圆心的圆。

P 轴则 C 点的纵坐标 PC 为单位(T 轴以 TC 为 单位) 。若已知在此过程中气体所经历的最低温度为 T0 ,则在此过程中,气体密 度的最大值 ρ1 和最小值 ρ2 之比 ρ1/ρ2 应等于多少? 【解说】本题物理知识甚简,应用“推论 1”即可。

P1 ?1T1 = P2 ? 2 T2 T ? ?1 ?2 = P1T2 P2 T1 = P1 / T1 P2 / T2 T 此式表明, P 越大时,ρ 就越大。

故本题归结为求 P 的极大值和极小值。 第 71 页 共 141 页 最新高中物理竞赛讲义(完整版) 方法一:P 与 T 的关系服从圆的方程(参数方程为佳) T = Tc rcosθ P = PC rsinθ 引入 y = P T = PC ? r sin ? TC ? r cos ? T ,然后求这个函数的极值… T 方法二:见图 6-11,从 P 的几何意义可知, P 等于状态点到原点的连线与 T 轴夹角的正切值, 求 P 的极大和极小归结为求这个正切值 T 的极大和极小——很显然,当直线与圆周的两处相切时, 出现了这样的极大和极小值。

θmax = α β ,θmin =α ? β 而 tgα= sinβ= PC TC r 2 2 TC ? PC ? tgβ= TC ? T0 2TCT0 (注意:依题意,r = TC ? T0 ) 所以 tgθmax = tg? ? tg? 1 ? tg?tg? tg? ? tg? 1 ? tg?tg? = PC 2TCT0 ? TC (TC ? T0 ) TC 2TCT0 ? PC (TC ? T0 ) PC 2TCT0 ? TC (TC ? T0 ) TC 2TCT0 ? PC (TC ? T0 ) PC 2TCT0 ? TC (TC ? T0 ) TC 2TCT0 ? PC (TC ? T0 ) tgθmin = = 【答案】 〔 PC 2TCT0 ? TC (TC ? T0 ) TC 2TCT0 ? PC (TC ? T0 ) 〕/〔 〕 。

d、道尔顿分压定律:当有 n 种混合气体混合在一个容器中时,它们产生的 压强等于每一种气体单独充在这个容器中时所产生的压强之和。

即 P = P1 P2 P3 … Pn 4、理想气体的内能、做功与吸放热计算 a、理想气体的内能计算 由于不计分子势能,故 E = N? ?K = N i kT = N 2 i R 2 NA T = ? i 2 RT ,其中 N 为分子总数, ? 为气体的摩尔数。

由于(对一定量的气体)内能是温度的单值函 数,故内能的变化与过程完全没有关系。

b、理想气体的做功计算 气体在状态变化时,其压强完全可以是变化的,所以气体压力的功从定义 角度寻求比较困难。但我们可以从等压过程的功外推到变压过程的功(☆无限分 割→代数累计…) ,并最终得出这样一个非常实用的结论:准静态过程理想气体 的功 W 总是对应 P-V 图象中的“面积” 。

这个面积的理解分三层意思—— ①如果体积是缩小的,外界对气体做功,面积计为正;②如果体积是增大 的,气体对外界做功,面积计为负;③如果体积参量变化不是单调的(例如循环 过程) ,则面积应计相应的差值。

如图 6-3 所示。 第 72 页 共 141 页 最新高中物理竞赛讲义(完整版) (☆学员思考:气体膨胀是不是一定对外做功?…) c、吸放热的计算 初中所学的通式 Q = cmΔT 仍适用,但值得注意的是,对固体和液体而言, 比热容 c 基本恒定(和材料相关) ,但对气体而言,c 会随着过程的不同而不同。

对理想气体,我们一般引进“摩尔热容”C(从克拉珀龙方程知,我们关心 气体的摩尔数更甚于关心气体的质量) ,物理意义:1 摩尔物质温度每升高 1K 所 吸收的热量。摩尔热容和比热容的关系 C = ΔT ②等压过程的摩尔热容称为“定压摩尔热容” ,用 CP 表示,所以 Q = ? CP ΔT 对于其它的复杂过程而言,摩尔热容的表达比较困难,因此,用直接的途 径求热量不可取,这时,我们改用间接途径:即求得ΔE 和 W 后,再用热力学第 一定律求 Q 。

(☆从这个途径不难推导出:① CV = i 2 cm ? 。 ①等容过程的摩尔热容称为“定容摩尔热容” ,用 CV 表示,所以 Q = ? CV R ,CP = i 2 R R ,即 CP = CV R … ;② E = ? CVT ) 【例题 8】0.

1mol 的单原子分子理想气体,经历如图 6-13 所示的 A→B→C →A 循环,已知的状态途中已经标示。

试问: (1)此循环过程中,气体所能达到的最高温度状态在何处,最高温度是多 少? (2)C→A 过程中,气体的内能增量、做功情 况、吸放热情况怎样? 【解说】 (1)介绍玻马定律的 P-V 图象,定性 预计 Tmax 的大概位置(直线 BC 上的某一点) 。

定量 计算 PV 的极大值步骤如下—— BC 的直线方程为 P = - 1 V 2 2 y = PV = - 1 V2 2V 2 显然,当 V = 2 时,y 极大,此时,P = 1 代入克拉珀龙方程:1?105?2?10-3 = 0.

1?8.31Tmax ,解得 Tmax = 240.7K (2)由克拉珀龙方程可以求得 TC = 180.

5K = TB ,TA = 60.2K ΔE = ? i 2 RΔT = 0.1? 3 ?8.31?(60.2-180.5) = -150.0J 2 第 73 页 共 141 页 最新高中物理竞赛讲义(完整版) 根据“面积”定式,W = 0.

5?105?2?10-3 = 100J 计算 Q 有两种选择:a、Q = ? CPΔT = 0.1? 5 ?8.31?(60.

2-180.5) = - 2 250.0J b、Q = ΔE - W = -250.0J 【答案】 (1)V = 2?10-3 时,Tmax 为 240.7K; (2)内能减少 150.0J,外界对 气体做功 100J,气体向外界放热 250J 。

〖思考一〗B→C 过程气体吸放热的情况又怎样? 〖解〗由于 B→C 过程一直是气体对外界做功,但内能却是先增后减,所以 过程的吸放热情况会复杂一些。

由ΔE = Q W 不难看出,TB 到 Tmax 阶段肯定是吸热,但在 Tmax 到 TC 阶段则无 法定性判断。所以这里启用定量方法—— 在 Tmax 到 TC 阶段取一个极短过程 V →(V ΔV) ,在此过程中 ΔE = ? i 2 RΔT = 2 3 2 Δ(PV)≈ 3 2 (PΔV VΔP) 2 由于 P = - 1 V 2 ,有ΔP = - 1 ΔV 故ΔE = 2 3 2 (2-V)ΔV 2 2 又 W = - 1 ΔV(P 〈P-ΔP〉 )= -PΔV 1 ΔPΔV ≈ -PΔV =( 1 V- 2)ΔV ( “过程极短”的缘故…) 所以 Q = ΔE-W =(5-2V)ΔV Q 2.

5 时开始吸热 (转变体积 V′= 2.5 -3 3 5 ?10 m ,对应转变压强 P′= 0.75?10 Pa ,转变温度 T′= 225.6K) 。 a、吸热阶段:ΔE = 0.

1? 3 ?8.31?(225.6-180.5)= 56.2J 2 W = - 1 (1.5 0.75)?105?(2.5-1)?10-3 = -168.8J 2 Q = ΔE-W = 225.

0J b、放热阶段:ΔE = 0.1? 3 ?8.31?(180.5-225.6)= -56.2J 2 W = - 1 (0.5 0.75)?105?(3-2.5)?10-3 = -31.3J 2 Q = ΔE-W = -24.

9J (说明:如果针对 B→C 全程计算,不难得出 Q = 200.0J 。那么,分出吸热、 放热的细节是不是没有必要呢?不能这样认为。因为热传递的过程具有不可逆 性,所以这里的热量“总帐”对气体可能是与“细帐”没有区别,但对外界而言, 吸热必然是来自高温热源,而放热却是针对低温热源,它们就象同一个公司的两 个不同贸易伙伴,算清具体往来显然是必要的。

) 〖答〗从高温热源吸收 225.

0J 的热量,向低温热源放出 24.9J 的热量。 〖思考二〗B→C 过程吸热过程和放热过程的摩尔热容分别是多少? 〖解答〗 解略。 吸热过程 C1 = 49.9J/(mol? K), 放热过程 C2 = 5.

54 J/(mol? K)。 〖思考三〗整个循环的效率是多少? 第 74 页 共 141 页 最新高中物理竞赛讲义(完整版) 〖解答〗 A→ B 过程吸热 Q = ? CV Δ T = 0.

1 ? 3 ? 8.31 ? (180.5 -60.2)= 2 150.0J ,B→C 过程吸热 225J ,C→A 过程只放热,所以全过程(从高温热源) 的吸热总量为 375J。 整个循环对外做的功就是△ABC 的面积,绝对值为 1 ?1.

0?105?2?10? 2 3 = 100J 所以,效率 η = W Q吸 = 100 375 = 26.7% 。 (从这个计算我们可以进一步领会区 分吸热和放热的重要性。

) 【例题 9】如图 6-14 所示,A 和 B 是两个圆筒形绝热容器,中间用细而短的 管子连接,管中有导热性能良好的阀门 K ,而管子和阀门对外界却是绝热的。F 是带柄的绝热活塞,与容器 A 的内表面紧密接触,不漏气,且不计摩擦。

开始时,K 关闭,F 处于 A 的左端。A 中有 ? 摩尔、温度为 T0 的理想气体,B 中则为真空。现向右推动 F ,直到 A 中气体的体积与 B 的容积相等。

在这个过 程中,已知 F 对气体做功为 W ,气体温度升为 T1 ,然后将 K 稍稍打开一点,使 A 中的气体缓慢向 B 扩散,同时让活塞 F 缓慢前进,并保持 A 中活塞 F 附近气体 的压强近似不变。

不计活塞、阀门、容器的 热容量,试问:在此过程中,气体最后的温 度 T2 是多少? 【解说】为求温度,可以依据能量关系 或状态方程。但事实证明,仅用状态方程还 不够,而要用能量关系,摩尔热容、做功的 寻求是必不可少的。

过程一:K 打开前,过程绝热,据热力学第一定律,ΔE = W 又由 E = ? CVT 知 ΔE = ? CV(T1 ? T0) 因此,CV = W ?(T1 ? T0 ) ?RT1 V1 ① ② 而且在末态,P1 = 过程二:K 打开后,过程仍然绝热,而且等压。

所以, W′= P1(V1 ? V1′) ,其中 V1′为 A 容器最终的稳定容积。

〖学员思考〗此处求功时ΔV 只取 A 容器中气体体积改变而不取整个气体的 体积改变,为什么?——因为 B 容器中气体为自由膨胀 的缘故… .... 为求 V1′,引进盖?吕萨克定律 从这两式可得 W′= P1V1 2T1 ? T2 T1 V1 T1 = ? V1 ? V1 T2 ③ 而此过程的 ΔE′= ? CVΔT = ? CV(T2 ? T1) ④ (注意:这里是寻求内能增量而非热量,所以,虽然是等压过程,却仍然用 CV 而非 CP) 最后,结合①②③④式对后过程用热力学第一定律即可。

【答案】T2 = 2?R (T1 ? T0 ) ? W ?R (T1 ? T0 ) ? W T1 。

第 75 页 共 141 页 最新高中物理竞赛讲义(完整版) 四、相变 相:热学系统中物理性质均匀的部分。系统按化学成分的多少和相的种类多 少可以成为一元二相系 (如冰水混合物) 和二元单相系 (如水和酒精的混合液体) 。

相变分气液相变、固液相变和固气相变三大类,每一类中又有一些具体的分支。 相变的共同热学特征是:相变伴随相变潜热。 1、气液相变,分气化和液化。气化又有两种方式:蒸发和沸腾,涉及的知识点 有饱和气压、沸点、汽化热、临界温度等。

a、蒸发。蒸发是液体表面进行的缓慢平和的气化现象(任何温度下都能进 行) 。影响蒸发的因素主要有①液体的表面积、②液体的温度、③通风条件。从 分子动理论的角度不难理解,蒸发和液化必然总是同时进行着,当两者形成动态 平衡时,液体上方的气体称为—— 饱和气,饱和气的压强称为饱和气压 PW 。

①同一温度下,不同液体的 PW 不同(挥发性大的液体 PW 大) ,但同种液体的 PW 有唯一值(与气、液的体积比无 关,与液体上方是否存在其它气体无关) ;②同一种液体,在不同的温度下 PW 不 同(温度升高,PW 增大,函数 PW = P0 e ? L RT ,式中 L 为汽化热,P0 为常量) 。

汽化热 L :单位质量的液体变为同温度的饱和气时所吸收的热量,它是相 变潜热的一种。汽化热与内能改变的关系 L = ΔE PW(V 气 ? V 液)≈ ΔE PWV 气 b、沸腾。

一种剧烈的汽化,指液体温度升高到一定程度时,液体的汽化将 不仅仅出现在表面,它的现象是液体内部或容器壁出现大量气泡,这些气泡又升 到液体表面并破裂。液体沸腾时,液体种类不变和外界压强不变时,温度不再改 变。

(从气泡的动力学分析可知)液体沸腾的条件是液体的饱和气压等于外界 压强。 (如在 1 标准大气压下,水在 100℃沸腾,就是因为在 100℃时水的饱和气 压时 760cmHg。

) 沸点,液体沸腾时的温度。①同一外界气压下,不同液体的沸点不同;② 同一种液体,在不同的外界气压下,沸点不同(压强升高,沸点增大) 。 c、液化。气体凝结成液体的现象。对饱和气,体积减小或温度降低时可实 现液化;对非饱和气,则须先使它变成饱和气,然后液化。

常用的液化方法:①保持温度不变,通过增大压强来减小气体的体积;② 保持体积不变,降低温度。 【例题 10】有一体积为 22.4L 的密闭容器,充有温度 T1 、压强 3atm 的空气 和饱和水汽,并有少量的水。

今保持温度 T1 不变,将体积加倍、压强变为 2atm , 这时容器底部的水恰好消失。将空气、饱和水汽都看成理想气体,试问: (1)T1 的值是多少?(2)若保持温度 T1 不变,体积增为原来的 4 倍,容器内的压强又 是多少?(3)容器中水和空气的摩尔数各为多少? 【解说】容器中的气体分水汽和空气两部分。

容器中压强与空气压强、水汽 压强的关系服从道尔顿分压定律。

对水汽而言,第二过程已不再饱和。 (1)在 T1 、3atm 状态,3 = P1 PW (P1 为空气压强) 在 T1 、2atm 状态,2 = P2 PW (P2 为空气压强) 第 76 页 共 141 页 最新高中物理竞赛讲义(完整版) 而对空气,P1V = P22V 解以上三式得 P1 = 2atm ,P2 = 1atm ,PW = 1atm ,可得 T1 = 100℃ = 373K (2)此过程的空气和水汽质量都不再改变,故可整体用玻-马定律:2?2V = P′4V (这里忽略了“少量的”水所占据的体积…) (3)在一过程的末态用克拉珀龙方程即可。

【答案】 (1)373K ; (2)1atm ; (3)均为 1.46mol 。 【例题 11】如图 6-15 所示,在一个横截面积为 S 的封闭容器中,有一质量 M 的活塞把容器隔成Ⅰ、Ⅱ两室,Ⅰ室中为饱和水蒸气,Ⅱ室中有质量为 m 的氮 气,活塞可以在容器中无摩擦地滑动。

开始时,容器被水平地放置在地面上,活 塞处于平衡,Ⅰ、Ⅱ两室的温度均为 T0 = 373K,压强为 P0 。现将整个容器缓慢 地转到竖直位置,两室的温度仍为 T0 ,但Ⅰ室中有少量水蒸气液化成水。

已知 水的汽化热为 L ,水蒸气和氮气的摩尔质量分别为μ1 和μ2 ,试求在整个过程 中,Ⅰ室内系统与外界交换的热量。

【解说】容器水平放置时,设水蒸气的体积为 V1 ,氮气的体积为 V2 ;直立 时,设有体积为ΔV 的水蒸气液化成水。 直立后水的饱和气在同温度下压强不变,故氮气的压强 P = P0- Mg S 在直立过程,对氮气用玻-马定律 P0V2 = P(V2 ΔV) 结合以上两式可得ΔV = Mg P0S ? Mg V2 m ?2 为解决 V2 ,对初态的氮气用克拉珀龙方程 P0V2 = 这样,ΔV = Mg P0S ? Mg RT0 ? mRT0 P0? 2 ?1P0 RT0 所以, 水蒸汽液化的质量 (用克拉珀龙方程) 为 Δm = 这部分水蒸气液化应放出热量 Q =Δm?L = 【答案】向外界放热 ?1 ? ?2 ?1 ?2 ΔV = ?1 ?2 ? mMg P0S ? Mg ? mMgL P0S ? Mg mMgL P0S ? Mg 。

〖思考〗解本题时,为什么没有考虑活塞对Ⅰ室做的功? 第 77 页 共 141 页 最新高中物理竞赛讲义(完整版) 〖答〗注意汽化热 L 的物理意义——它其中已经包含了气体膨胀(汽化)或 收缩(液化)所引起的做功因素,若再算做功,就属于重复计量了。

〖*再思考〗Ⅱ中氮气与“外界”交换的热量是多少? 〖 * 答〗氮气没有相变,就可直接用热力学第一定律。

Δ E = 0 , W = ? m ?2 RT0ln V2 ? ?V = ? V2 m ?2 RT0ln ( 1 Mg P0S ? Mg ) ,所以 Q = Δ E – W = m ?2 RT0ln (1 Mg P0S ? Mg ) ,吸热。

2、湿度与露点 a、空气的湿度。表示空气干湿程度的物理量,有两种定义方式。

①绝对湿 度:空气中含有水蒸气的压强;②相对湿度 B :空气中含有水蒸气的压强跟该 温度下水的饱和蒸气压的比值,即 B = P PW ?100%(相对湿度反映了空气中水蒸 气离开饱和的程度,人体感知的正是相对湿度而非绝对湿度,以 B 值为 60~70% 比较适宜。

在绝对湿度一定的情况下,气温升高,B 值减小——因此,夏天尽管 绝对湿度较大,但白天仍感到空气比晚上干燥) 。 b、露点:使空气中的水蒸气刚好达到饱和的温度。

露点的高低与空气中含 有水蒸气的压强(即绝对湿度)密切相关,根据克拉珀龙方程,也就是与空气中 水蒸气的量有关:夏天,空气中水蒸气的量大,绝对湿度大(水蒸气的压强大) , 对应露点高;反之,冬天的露点低。

3、固液相变,分熔解和凝固。 a、熔解。物质从故态变成液态。晶体有一定的熔解温度——熔点(严格地 说,只有晶体才称得上是固体) ,非晶体则没有。大多数物质熔解时体积会膨胀, 熔点会随压强的增大而升高,但也有少数物质例外(如水、灰铸铁、锑、铋等, 规律正好相反) 。

(压强对熔点的影响比较微弱,如冰的熔点是每增加一个大气压 熔点降低 0.0075℃。 ) 熔解热 λ:单位质量的晶体在溶解时所吸收的热量。

从微观角度看,熔解 热用于破坏晶体的空间点阵, 并最终转化为分子势能的增加, 也就是内能的增加, 至于体积改变所引起的做功,一般可以忽略不计。 b、凝固。

熔解的逆过程,熔解的规律逆过来都适用与凝固。 4、固气相变,分升华和凝华。 a、升华。物质从固态直接变为气态的过程。在常温常压下,碘化钾、樟脑、 硫磷、干冰等都有显著的升华现象。 升华热:单位质量的物质在升华时所吸收的热量。

(从微观角度不难解释) 升华热等于同种物质的汽化热和熔解热之和。 b、凝华。升华的逆过程。如打霜就是地面附近的水蒸气遇冷(0℃以下)凝 华的结果。凝华热等于升华热。 5、三相点和三相图 亦称 “三态点” 。

一般指各种稳定的纯物质处于固态、 液态、 气态三个相 (态) 平衡共存时的状态,叫做该物质的“三相点”。该点具有确定的温度和压强(清 注意:两相点,如冰点和汽点并不具备这样的特征)。

所以三相点这个固定温度 适于作为温标的基点,现在都以水的三相点的温度作为确定温标的固定点。 附:几种物质的三相点数据 温度(K) 第 78 页 共 141 页 压强(Pa) 最新高中物理竞赛讲义(完整版) 氢 氘 氖 氮 二氧化碳 水 13.

84 18.63 24.57 63.18 216.55 273.16 7038.2 17062.4 43189.2 12530.2 517204 610.

5 怎样理解三相点的存在呢?将相变的气 化曲线 OK(即饱和气压随温度变化的曲线— —对应函数 PW = P0 e ? L RT ) 、溶解曲线 OL(压强 随熔点变化的曲线) 、升华曲线 OS(压强随升 华点变化的曲线) 描绘在同一个 P-t 坐标中, 就构成“三相图” 。

三条曲线的交点就是三相 点,如图 6-16 所示。 在图中,为了表示三相点的精确位置,坐 标的标度并不是均匀的, 所以坐标轴用虚线表 示。

OK、OL 和 OS 事实上分别是水汽两相点、 冰水两相点和冰汽两相点 “运动” 的结果—— 也就是相应两相的分界线。 五、固体和液体 1、固体——晶体和非晶体 a、晶体和非晶体的根本区别是:是否具有固定的熔点。

晶体又分为单晶体 和多晶体,单晶体(如石英、云母、明矾、冰等)还具有规则的几何形状、物理 性质上表现为各向异性;多晶体(如岩石、金属等)则和非晶体一样,无规则几 何形状、各向同性。

b、空间点阵:组成晶体的微观粒子所形成的规则排列(非晶体没有空间点 阵) 。晶体之所以具有固定的熔点,是因为发生相变时,吸收的热量全部用来破 坏空间点阵结构——分子间距的改变导致分子势能增大, 而分子的平均动能则不 变。

2、液体的表面张力 a、表面张力:存在于液体表面的使表面收缩的力。表面张力的微观解释是: 蒸发使表面分子间距大于 r0 ,因此分子力体现为引力。 表面张力系数α:设想在液面作长为 L 的线段,则线段两边表面张力必垂 直于这条线段,且于液面相切,各自的大小均为 f = αL ,其中α称表面张力 系数。

b、浸润现象:液体与固体接触时,若接触角θ (见图 6-17)为锐角,称为浸润现象;反之,接触 角为钝角, 称为不浸润。

液体相对固体是否浸润取决 于液体和固体的组合关系, 如水能浸润玻璃却不能浸 第 79 页 共 141 页 最新高中物理竞赛讲义(完整版) 润石蜡,水银能浸润锌版却不能浸润玻璃。

当θ= 0 时,称为“完全浸润” ;当θ=π时,称为“完全不浸润” 。 从微观角度看,液体能否浸润固体取决于液体与固体接触的“附着层”分 子受液体分子力(内聚力)更大还是受固体分子力(附着力)更大。

c、毛细现象:浸润管壁的液体在毛细管中液面升高,不浸润管壁的液体在 毛细管中液面降低的现象。毛细现象的形成事实上是液体表面张力的合效果。 ☆如果毛细管的为 r ,液体的表面张力系数为α,对管壁的浸润角为θ,不 难求出毛细现象导致的液面上升(或下降)量 h = 2 cos ? ?gr 。

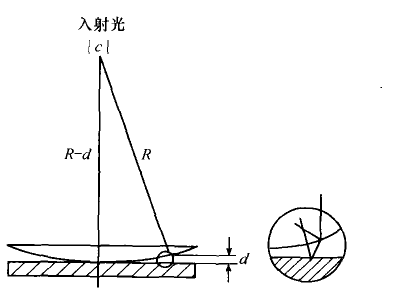
【例题 12】如图 6-18 所示,在一个两端开口的、半径为 1mm 的长 毛细管中装满水,然后把它竖直地放在空间,认为水完全浸润毛细管, 且水的表面张力系数为 7.

3?10-2N/m , 则留在管中的水柱应有多长? 【解说】由于有两个曲面,故曲面边缘的表面张力合力为 F = 2?α2πrcosθ 液柱的重力 G =ρπr2hg 解它们的平衡方程即可(θ= 0) -2 【答案】h = 2.

94?10 m 。 第八部分 静电场 第一讲 基本知识介绍 在奥赛考纲中,静电学知识点数目不算多,总数和高考考纲基本相同,但在 个别知识点上,奥赛的要求显然更加深化了:如非匀强电场中电势的计算、电容 器的连接和静电能计算、电介质的极化等。

在处理物理问题的方法上,对无限分 割和叠加原理提出了更高的要求。

如果把静电场的问题分为两部分,那就是电场本身的问题、和对场中带电体 的研究,高考考纲比较注重第二部分中带电粒子的运动问题,而奥赛考纲更注重 第一部分和第二部分中的静态问题。

也就是说,奥赛关注的是电场中更本质的内 容,关注的是纵向的深化和而非横向的综合。 一、电场强度 1、实验定律 a、库仑定律 内容; 条件:⑴点电荷,⑵真空,⑶点电荷静止或相对静止。事实上,条件⑴和 ⑵均不能视为对库仑定律的限制, 因为叠加原理可以将点电荷之间的静电力应用 第 80 页 共 141 页 最新高中物理竞赛讲义(完整版) 到一般带电体,非真空介质可以通过介电常数将 k 进行修正(如果介质分布是均 匀和“充分宽广”的,一般认为 k′= k /εr) 。

只有条件⑶,它才是静电学的基 本前提和出发点(但这一点又是常常被忽视和被不恰当地“综合应用”的) 。 b、电荷守恒定律 c、叠加原理 2、电场强度 a、电场强度的定义 电场的概念;试探电荷(检验电荷) ;定义意味着一种适用于任何电场的对 电场的检测手段;电场线是抽象而直观地描述电场有效工具(电场线的基本属 性) 。

b、不同电场中场强的计算 决定电场强弱的因素有两个:场源(带电量和带电体的形状)和空间位置。

这可以从不同电场的场强决定式看出—— ⑴点电荷:E = k Q 2 r 结合点电荷的场强和叠加原理,我们可以求出 任何电场的场强,如—— ⑵均匀带电环,垂直环面轴线上的某点 P:E = kQr (r ? R 2 ) 2 3 2 ,其中 r 和 R 的意义见图 7-1。

⑶均匀带电球壳 内部:E 内 = 0 外部:E 外 = k Q ,其中 r 指考察点到球心的距离 2 r 如果球壳是有厚度的的(内径 R1 、外径 R2) ,在壳体 中(R1<>R)的 地方放一个电量为 q 的点电荷,它受到的电场力将为多大? 〖解说〗上面解法的按部就班应用… 〖答〗 4 πkρq〔 R2 ? 3 3 b R?3 (b ? a ) 2 〕 。

二、电势、电量与电场力的功 【物理情形 1】如图 7-8 所示,半径为 R 的圆环均匀带电,电荷线密度为λ, 圆心在 O 点,过圆心跟环面垂直的轴线上有 P 点, PO = r , 以无穷远为参考点,试求 P 点的电势 UP 。

【模型分析】这是一个电势标量叠加的简单模型。先在圆 环上取一个元段ΔL ,它在 P 点形成的电势 ΔU = k ??L R2 ? r2 环共有 2?R 段, 各段在 P 点形成的电势相同, 而且它们是标 ?L 量叠加。

【答案】UP = 2?k?R R2 ? r2 〖思考〗 如果上题中知道的是环的总电量 Q , 则 UP 的结论为多少?如果这个 总电量的分布不是均匀的,结论会改变吗? 〖答〗UP = kQ R2 ? r2 ;结论不会改变。

〖再思考〗将环换成半径为 R 的薄球壳,总电量仍为 Q ,试问: (1)当电量 均匀分布时,球心电势为多少?球内(包括表面)各点电势为多少?(2)当电 量不均匀分布时,球心电势为多少?球内(包括表面)各点电势为多少? 第 85 页 共 141 页 最新高中物理竞赛讲义(完整版) 〖解说〗 (1)球心电势的求解从略; 球内任一点的求解参看图 7-5 ΔU1 = k ??S1 = k ? ? ?? ? r1 = k?ΔΩ 2 r1 r1 cos? r1 cos ? ΔU2 = k?ΔΩ r2 cos ? cos ? 它们代数叠加成 ΔU = ΔU1 ΔU2 = k?ΔΩ r1 ? r2 而 r1 r2 = 2Rcosα 所以 ΔU = 2Rk?ΔΩ 所有面元形成电势的叠加 ΣU = 2Rk?ΣΔΩ 注意:一个完整球面的ΣΔΩ = 4π(单位:球面度 sr) ,但作 为对顶的锥角,ΣΔΩ只能是 2π ,所以—— ΣU = 4πRk?= k Q R (2)球心电势的求解和〖思考〗相同; 球内任一点的电势求解可以从(1)问的求解过程得到结论的反 证。

〖答〗 (1)球心、球内任一点的电势均为 k Q ; (2)球心电势仍为 k Q , R R 但其它各点的电势将随电量的分布情况的不同而不同(内部不再是等势体,球面 不再是等势面) 。

【相关应用】如图 7-9 所示,球形导体空腔内、外壁的 半径分别为 R1 和 R2 ,带有净电量 q ,现在其内部距球心为 r 的地方放一个电量为 Q 的点电荷,试求球心处的电势。

【解析】由于静电感应,球壳的内、外壁形成两个带电 球壳。球心电势是两个球壳形成电势、点电荷形成电势的合 效果。

根据静电感应的尝试,内壁的电荷量为-Q ,外壁的电 荷量为 Q q ,虽然内壁的带电是不均匀的,根据上面的结 论,其在球心形成的电势仍可以应用定式,所以… 【答案】Uo = k Q - k r Q R1 k Q?q 。

R2 〖反馈练习〗如图 7-10 所示,两个极薄的同心导体球壳 A 和 B,半径分别为 RA 和 RB ,现让 A 壳接地,而在 B 壳的外部距球心 d 的地方放一个电量为 q 的点 电荷。

试求: (1)A 球壳的感应电荷量; (2)外球壳的电势。 〖解说〗 这是一个更为复杂的静电感应情形, B 壳将 形成图示的感应电荷分布(但没有净电量) ,A 壳的情形 未画出 (有净电量) , 它们的感应电荷分布都是不均匀的。

此外,我们还要用到一个重要的常识:接地导体(A 壳)的电势为零。但值得注意的是,这里的“为零”是 一个合效果 ,它是点电荷 q 、A 壳、B 壳(带同样电荷 .

.. 时)单独存在时 在 A 中形成的的电势的代数和,所以, ..... 当我们以球心 O 点为对象,有 第 86 页 共 141 页 最新高中物理竞赛讲义(完整版) UO = k q k Q A k Q B = 0 d RA RB QB 应指 B 球壳上的净电荷量,故 QB = 0 所以 QA = - R A q d ☆学员讨论:A 壳的各处电势均为零,我们的方程能不能针对 A 壳表面上的 某点去列?(答:不能,非均匀带电球壳的球心以外的点不能应用定式!

) 基于刚才的讨论,求 B 的电势时也只能求 B 的球心的电势(独立的 B 壳是等 势体,球心电势即为所求)—— UB = k q k Q A d RB d d 〖答〗 (1)QA = - R A q ; (2)UB = k q (1- R A ) 。

RB 【物理情形 2】图 7-11 中,三根实线表示三根首尾相连的等长绝缘细棒,每 根棒上的电荷分布情况与绝缘棒都换成导体棒时完全相同。

点 A 是 Δabc 的中心, 点 B 则与 A 相对 bc 棒对称,且已测得它们的电势分别为 UA 和 UB 。试问:若将 ab 棒取走,A、B 两点的电势将变为多少? 【模型分析】 由于细棒上的电荷分布既不均匀、 三根细棒也没有构成环形, 故前面的定式不能直接 应用。

若用元段分割→叠加,也具有相当的困难。 所以这里介绍另一种求电势的方法。

每根细棒的电荷分布虽然复杂,但相对各自的 中点必然是对称的,而且三根棒的总电量、分布情 况彼此必然相同。这就意味着:①三棒对 A 点的电 势贡献都相同(可设为 U1) ;②ab 棒、ac 棒对 B 点 的电势贡献相同(可设为 U2) ;③bc 棒对 A、B 两点 的贡献相同(为 U1) 。

所以,取走 ab 前 3U1 = UA 2U2 U1 = UB 取走 ab 后,因三棒是绝缘体,电荷分布不变,故电势贡献不变,所以 UA′= 2U1 UB′= U1 U2 【答案】UA′= 2 3 UA ;UB′= 1 6 UA 1 2 UB 。

〖模型变换〗正四面体盒子由彼此绝缘的四块导体板构成,各导体板带电且 电势分别为 U1 、U2 、U3 和 U4 ,则盒子中心点 O 的电势 U 等于多少? 〖解说〗此处的四块板子虽然位置相对 O 点具有对称性,但电量各不相同, 因此对 O 点的电势贡献也不相同,所以应该想一点办法—— 我们用“填补法”将电量不对称的情形加以改观:先将每一块导体板复制三 块,作成一个正四面体盒子,然后将这四个盒子位置重合地放置——构成一个有 四层壁的新盒子。

在这个新盒子中,每个壁的电量将是完全相同的(为原来四块 板的电量之和) 、电势也完全相同(为 U1 U2 U3 U4) ,新盒子表面就构成了 一个等势面、整个盒子也是一个等势体,故新盒子的中心电势为 U′= U1 U2 U3 U4 第 87 页 共 141 页 最新高中物理竞赛讲义(完整版) 最后回到原来的单层盒子,中心电势必为 U = 〖答〗U = 1 4 1 4 U′ (U1 U2 U3 U4) 。

☆学员讨论:刚才的这种解题思想是否适用于“物理情形 2”?(答:不行, 因为三角形各边上电势虽然相等,但中点的电势和边上的并不相等。 ) 〖反馈练习〗电荷 q 均匀分布在半球面 ACB 上,球面半径为 R ,CD 为通过 半球顶点 C 和球心 O 的轴线,如图 7-12 所示。

P、Q 为 CD 轴线上相对 O 点对称 的两点,已知 P 点的电势为 UP ,试求 Q 点的电势 UQ 。 〖解说〗这又是一个填补法的应用。

将半球 面补成完整球面,并令右边内、外层均匀地带上 电量为 q 的电荷,如图 7-12 所示。 从电量的角度看, 右半球面可以看作不存在, 故这时 P、Q 的电势不会有任何改变。

而换一个角度看,P、Q 的电势可以看成是两 者的叠加: ①带电量为 2q 的完整球面; ②带电量 为-q 的半球面。 考查 P 点,UP = k 2q U 半球面 R 其中 U UQ 半球面 显然和为填补时 Q 点的电势大小相等、符号相反,即 U 半球面 = - 以上的两个关系已经足以解题了。

〖答〗UQ = k 2q - UP 。 R 【物理情形 3】如图 7-13 所示,A、B 两点相距 2L ,圆弧 OCD 是以 B 为圆心、 L 为半径的半圆。

A 处放有电量为 q 的电荷, B 处放有电量为-q 的点电荷。 试问: ? (1)将单位正电荷从 O 点沿 OCD 移到 D 点,电场力对它做了多少功?(2)将单 位负电荷从 D 点沿 AB 的延长线移到无穷远处 去,电场力对它做多少功? 【模型分析】电势叠加和关系 WAB = q(UA - UB)= qUAB 的基本应用。

UO = k q k ?q = 0 L L ? UD = k q 3L k ?q = - 2 kq L 3L U∞ = 0 再用功与电势的关系即可。

【答案】 (1) 2 kq ; (2) 2 kq 。

3L 3L 【相关应用】在不计重力空间,有 A、B 两个带电小球,电量分别为 q1 和 q2 , 质量分别为 m1 和 m2 ,被固定在相距 L 的两点。试问: (1)若解除 A 球的固定, 它能获得的最大动能是多少?(2)若同时解除两球的固定,它们各自的获得的 最大动能是多少?(3)未解除固定时,这个系统的静电势能是多少? 【解说】第(1)问甚间;第(2)问在能量方面类比反冲装置的能量计算, 第 88 页 共 141 页 最新高中物理竞赛讲义(完整版) 另启用动量守恒关系;第(3)问是在前两问基础上得出的必然结论…(这里就 回到了一个基本的观念斧正:势能是属于场和场中物体的系统,而非单纯属于场 中物体——这在过去一直是被忽视的。

在两个点电荷的环境中,我们通常说“两 个点电荷的势能”是多少。 ) 【答】 (1)k q1q 2 ; (2)Ek1 = r m2 m1 ? m 2 k q1q 2 ,Ek2 = r m1 m1 ? m 2 k q1q 2 ; (3)k q1q 2 。

r r 〖思考〗设三个点电荷的电量分别为 q1 、q2 和 q3 ,两两相距为 r12 、r23 和 r31 ,则这个点电荷系统的静电势能是多少? 〖解〗略。

〖答〗k( q1q 2 q2q3 q 3q1 ) 。 r12 r23 r31 〖反馈应用〗如图 7-14 所示,三个带同种电荷的相同金属小球,每个球的 质量均为 m 、电量均为 q ,用长度为 L 的三根绝缘轻绳连接着,系统放在光滑、 绝缘的水平面上。

现将其中的一根绳子剪断, 三个球将开始 运动起来,试求中间这个小球的最大速度。 〖解〗设剪断的是 1、3 之间的绳子,动力学分析易知, 2 球获得最大动能时,1、2 之间的绳子与 2、3 之间的绳子 刚好应该在一条直线上。

而且由动量守恒知, 三球不可能有 沿绳子方向的速度。 设 2 球的速度为 v , 1 球和 3 球的速度 为 v′,则 动量关系 mv 2m v′= 0 能量关系 3k q 2 L = 2 kq 2 L k q2 2L 1 2 mv2 1 2 2m v? 2 解以上两式即可的 v 值。

〖答〗v = q 2k 3mL 。 三、电场中的导体和电介质 【物理情形】两块平行放置的很大的金属薄板 A 和 B,面积都是 S ,间距为 d(d 远小于金属板的线度) ,已知 A 板带净电量 Q1 ,B 板带尽电量 Q2 ,且 Q2