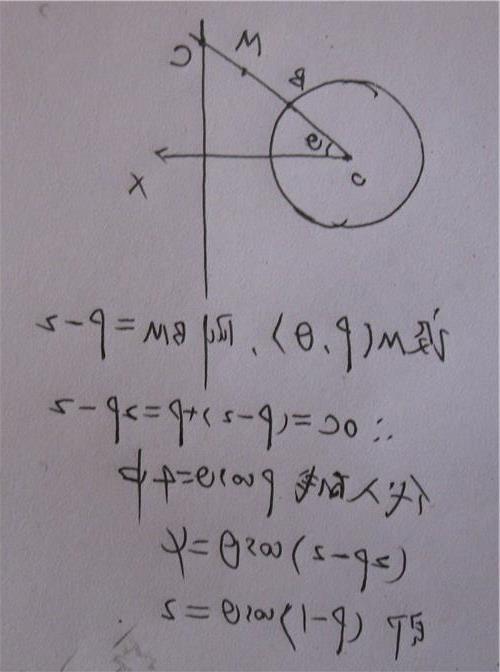笛卡尔坐标 极坐标——从笛卡尔的心形线说起
解析几何之父笛卡尔因数学与瑞典公主克里斯汀结缘,在交流数学的过程中互生爱慕之心。但身份的悬殊和年龄的差距使得他们不能为世人所容,笛卡尔被瑞典国王流放了。两人从此断绝了联系,在相思煎熬中,笛卡尔的身体每况愈下。
临近生命的终点,他向公主发出了最后一封信,内容只有一个方程ρ=α(1-sinθ)。当众人均对其不甚了了的时候,信件终于辗转到了公主的手中。打开信件的她刹那间泪流满面,原来这个方程对应的图形是一颗心。通过这封信,公主终于知道笛卡尔至死未对她忘情。对这个浪漫的故事,人们不再愿意追究它的真实性,却为他们忠贞不渝的爱情而扼腕不已。
实际上,信上只是一个极坐标方程。说起极坐标,首先得从极坐标系的建立说起。众所周知,利用代数方法解决几何问题的关键是将图形放置在坐标系中。在所有坐标系中最为常见是直角坐标系,但随着问题的逐步加深人们发现有些问题在直角坐标系中很难解决甚至无法解决,由此极坐标系应运而出。
所谓极坐标,在平面上取定点ο,自点ο引射线οx,同时确定一个长度单位和计算角度的正方向(通常取逆时针方向为正方向),这就建立了一个极坐标系。
其中,点ο称为极点,射线οx称为极轴。据此,在极坐标系中确定一点m的坐标需要两个量:极径ρ与极角θ。其中ρ为线段om的长度,θ表示以射线οx为始边,射线om为终边所成的角。如果一条曲线上任意一点极坐标适合方程(ρ,θ)=0;并且极坐标适合方程(ρ,θ)=0的点都在曲线上。那么这个方程称为这条曲线的极坐标方程。
以平面直角坐标系的原点ο为极点,x轴的正半轴为极轴,且在两种坐标系中取相同的长度单位,平面内任意一点p的直角坐标(x,y)与极坐标(ρ,θ)可以互相转化,其转化关系为:及
。例如圆m的普通方程为x2 y2=1,那么它的极坐标方程为ρ=1;再如极坐标系中经过点b(5,π),且垂直于极轴的直线方程为ρcosθ=-5,则其普通方程为x=-5。
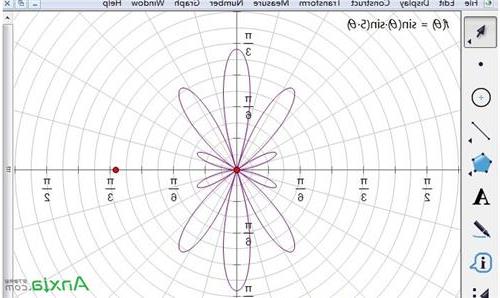
极坐标产生迄今,前人发现很多兼具数学抽象美与形象美的极坐标方程。其中最著名的有圆锥曲线ρ=■、玫瑰线ρ=acos(kθ)或ρ=asin(kθ)、阿基米德螺线ρ=a bθ等。
天文学中著名的开普勒第二定律在极坐标背景下能够很好地解决。除此之外,极坐标在定位与导航及建模方面也有非常广泛的应用。(省镇江一中刘银)