狄拉克函数导数 狄拉克梳状函数(图)

2017-11-09
字体:
大中小
浏览:
文章简介：狄拉克梳状函数(图) 上一回说到,单位冲激函数有诸多妙用.在数字信息技术时代,由单位冲激 函数派生出的狄拉克梳状函数用途更广.本文专门介绍如

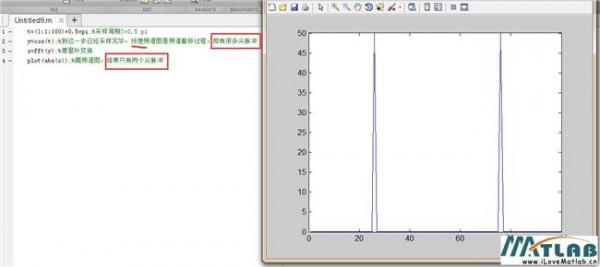
狄拉克梳状函数(图) 上一回说到,单位冲激函数有诸多妙用。在数字信息技术时代,由单位冲激 函数派生出的狄拉克梳状函数用途更广。本文专门介绍如下: 狄拉克梳状函数的定义式为 (1 ) 其时域波形是周期为 T 的单位冲激串,所以也称为理想抽样函数,如下图 所示: 图 1 狄拉克梳状函数的时域波形 我们当然可以按周期函数的傅立叶级数方法求其频谱。

其傅立叶系数为 (2 ) 所以其傅立叶级数展开式为 (3 ) 可见其频率成分只分布在 ω=nω1 (n=0,±1,±2,…)的离散频点,各 频率分量幅度值均为 1/T 。

其双边频谱图如下: 图 2 狄拉克梳状函数的傅立叶系数 其频谱为离散频谱,谱线高度为 1/T,频率间隔为 ω1=2π/T 。

其实引进了冲激函数的概念之后, 对一般周期函数也可以求其傅里叶变换为 (4 ) 其中 Cn 为周期函数的傅立叶系数。 所以根据式(4)和(2),可以用傅里叶变换直接对狄拉克梳状函数式(1) 求其频谱函数 (5 ) 其频谱图如下: 图 3 狄拉克梳状函数的傅里叶变换 可见狄拉克梳状函数的傅里叶变换仍然是频域的狄拉克梳状函数, 频谱冲激 串的周期是基频 ω1 ,并且冲激强度也均为 ω1 。

用狄拉克梳状函数表示离散信号和离散频谱, 将给信号分析和处理带来极大 的方便。详情且听下回分解。