笛卡尔函数图像 教您在几何画板极坐标系画美丽的函数图像

2018-03-11
字体:
大中小
浏览:
文章简介：极坐标系是指在平面内由极点.极轴和极径组成的坐标系.在数学中我们不仅仅会学到一般的平面直角坐标系,也会学习空间坐标系,也少不了要学习极坐标.

极坐标系是指在平面内由极点、极轴和极径组成的坐标系。在数学中我们不仅仅会学到一般的平面直角坐标系,也会学习空间坐标系,也少不了要学习极坐标。在解数学题时也时常会用到极坐标系,下面就通过举例利用极坐标系画函数来介绍几何画板极坐标系的强大之处。

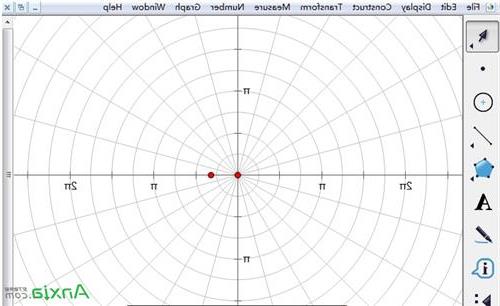
步骤一 建立极坐标系。打开几何画板,点击上方“绘图”菜单,在其下拉菜单选择“坐标网格”——“极坐标网格”命令,此时就建立好了极坐标系。


在几何画板中建立极坐标系示例

步骤二 建立三角坐标轴。鼠标在坐标系任意位置右键,在弹出的快捷选项下选择“三角坐标轴”,在弹出的对话框点击“是”,这样就在极坐标系中建立了三角坐标轴,如下图所示。


在几何画板中建立三角坐标轴示例

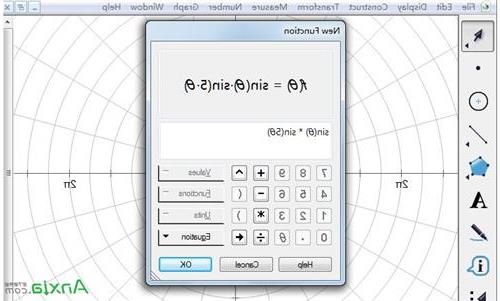
步骤三 绘制函数图像。点击上方的“绘图”菜单,在其下拉菜单选择“绘制新函数”命令,这样就弹出的新建函数对话框,输入如下图所示的函数表达式,然后点击“确定”。


在绘制新函数下输入函数表达式示例

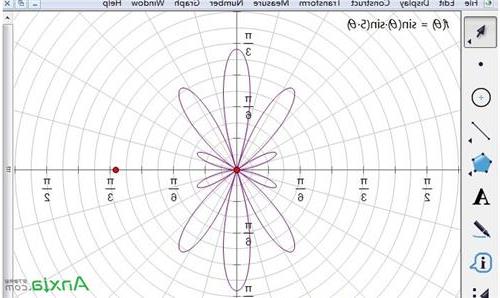
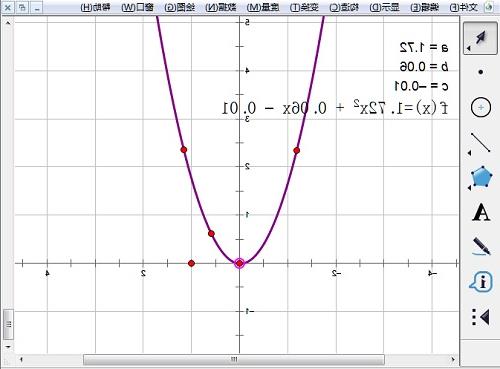
步骤四 这样就完成关于三角函数乘积的新函数图像的绘制,最终函数图像如下图所示。


在几何画板中绘制的函数图像示例

以上给大家讲解了几何画板中在极坐标系下绘制三角函数乘积的新函数图像的方法,利用这样的方法,可以画出很多有意思的函数图像,比如前面教程学习的笛卡尔心形函数,也是在极坐标下绘制的,如果有疑问,可参考教程:如何用几何画板画笛卡尔心形函数。