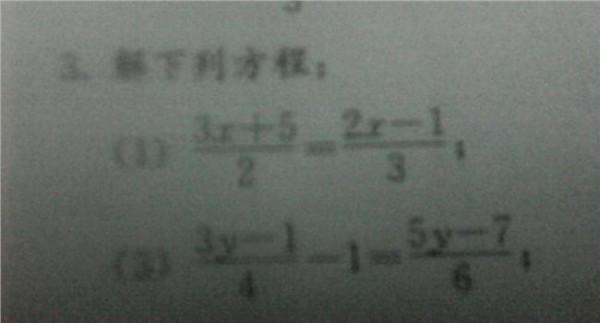解方程的步骤及格式 二元一次方程的解法及格式
概念 如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫做二元一次方程,有无穷个解,若加条件限定有有限个解.二元一次方程组,则一般有一个解,有时没有解,有时有无数个解.如一次函数中的平行,.
二元一次方程的一般形式:ax by c=0其中a、b不为零.这就是二元一次方程的定义.二元一次方程组定义:两个结合在一起的共含有两个未知数的一次方程,叫二元一次方程组. 常用方法 代入消元法, 加减消元法, 解法步骤 例题 {x-y=3 ① {3x-8y=4② 由①得x=y 3③ ③代入②得 3(y 3)-8y=4 y=1 所以x=4 则:这个二元一次方程组的解 {x=4 {y=1 实用方法: (一)加减-代入混合使用的方法.
例1,{13x 14y=41 (1) {14x 13y=40 (2) (2)-(1)得 x-y=-1 即x=y 1 (3) 把(3)代入(1)得 13(y-1) 14y=41 所以13y-13 14y=41 27y=54 y=2 把y=2代入(3)得 即x=1 所以:x=1,y=2 最后 x=1 ,y=2,解出来 特点:两方程相加减,单个x或单个y,这样就适用接下来的代入消元.
(二)换元法 是二元一次方程的另一种方法,就是说把一个方程用其他未知数表示,再带入另一个方程中 如: x y=590 y 20=90%x 代入后就是: x 90%x-20=590 例2:(x 5) (y-4)=8 (x 5)-(y-4)=4 令x 5=m,y-4=n 原方程可写为 m n=8 m-n=4 解得m=6,n=2 所以x 5=6,y-4=2 所以x=1,y=6 特点:两方程中都含有相同的代数式,如题中的x 5,y-4之类,换元后可简化方程也是主要原因.
(三)参数换元 例3,x:y=1:4 5x 6y=29 令x=t,y=4t 方程2可写为:5t 24t=29 29t=29 t=1 所以x=1,y=4 此外,还有代入法可做题.
x y=5 3x 7y=-1 x=5-y 3(5-y) 7y=-1 15-3y 7y=-1 4y=-16 y=-4 得:{x=9 {y=-4 houqbnpt 2014-10-12