悬赏期限将至 哥德巴赫猜想百万巨奖无人能拿?
但毫无疑问的是,这两年来,中国的一些数学爱好者们对这一猜想的证明始终没有放弃。其中一位叫敢峰的老先生具有一定的典型性。敢峰先生自称研究哥德巴赫猜想多年,并且在他担任主编的《教育世纪》杂志创刊号上发表了他的关于哥德巴赫猜想证明的文章。
据了解,这两年几乎每个星期都有来自全国各地的声称证明了这个猜想的材料寄到中科院数学与系统科学研究院,中科院数学与系统科学研究院科研处长陆柱家研究员说:“多的时候,一周能收到将近10封材料。”
在这些业余研究者中,各种身份都有,既有中学老师,也有企业高工。业余研究者中,有些人缺乏基本的数学知识,甚至把哥氏猜想的“1+1”表示为“1+1=2”;有的人说可以根据《易经》之所谓“太极生两仪,两仪生四象,四象生八卦”的原理,找到解决问题的办法。当然也有不少人在努力寻找他们自认为的科学的解决办法。
但是陆柱家研究员对此并不看好。他说:“在一些稍微象样的‘证明’中,基本都是一种思路,即任一偶数(自然数)可以写为2n,这里n是一个自然数,2n可以表示为n个不同形式的一对自然数之和:2n=1+(2n-1)=2+(2n-2)=3+(2n-3)=…=n+n,在筛去不适合哥德巴赫猜想结论的所有那些自然数对之后(例如1和2n-1;2i和(2n-2i),i=1,2,…;3j和(2n-3j),j=2,3,…;等等),如果能够证明至少还有一对自然数未被筛去,例如记其中的一对为p1和p2,那么p1和p2都是素数,即得n=p1+p2,这样哥德巴赫猜想就被证明了。
前一部分的叙述是很自然的想法。关键就是要证明‘至少还有一对自然数未被筛去’。目前世界上谁都未能对这一部分加以证明。要能证明,这个猜想也就解决了。”
哥德巴赫猜想表述简单是吸引业余研究者的重要因素
中国人对于哥德巴赫猜想的了解是由于陈景润的研究和作家徐迟的那篇著名的报告文学。1966年,陈景润发表了证明1+2的提要(发表在《科学通报》,17(1966),385-386页;黑体字是其原文中的用词),1973年,陈又在国内的《中国科学》杂志(第二期,111-128页)上公开发表了证明“1+2”的全文,这使得中国人在这个问题上取得了世界上的最好结果。
可惜的是,由于后来陈景润疾病缠身,不再允许他做更进一步的证明。
几十年来,许多数学家都在研究哥氏猜想,但是到目前为止,他们的成就尚未超过陈景润。
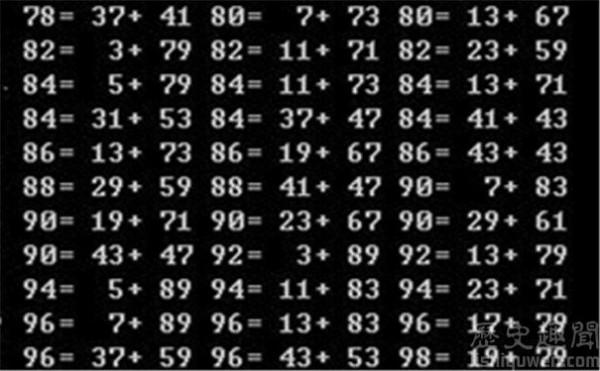
在专业数学家做研究的同时,为什么会有那么多的“民间数学家”也在孜孜不倦?陆柱家认为这主要还是因为哥德巴赫猜想的表述通俗易懂,“一般的数学题是很难看懂的,但是哥德巴赫猜想的表述很简单,那就是任何不小于6的偶数,都是两个奇素数之和,简称1+1。”也许表述上的简单,使好多人对这一问题的解决难度缺乏一个清醒的认识程度。
当然,在这些“民间数学家”中,的确有许多是数学痴迷者,“但是可以说,业余研究者是无法证明这个猜想的,除非世界一流的数学家,否则无法求证。”陆柱家说。也许在这个世界上,只有为数不多的几个人才能渡过这片智力的海洋。
没有一定的数学修养根本无法攻克这一难题
在众多“民间数学家”中,也不能否定有些人的积极性是在100万美元的悬赏之下产生的。当时两家出版社向世人提出这个挑战,是为了给希腊作家阿波斯托洛斯·多克西亚迪斯的小说《彼得罗斯大叔和哥德巴赫猜想》制造舆论声势。就连出版商费伯也说,估计世界上只有20个人有能力解答这个数学猜想。
事实上,许多人认为,“百万奖金”的时限只有两年,难免给人一种哗众取宠之感,大家知道,1908年所设悬赏求证费马大定理的奖金时限是100年。而数学的严谨性,也许决定了它不大可能在重奖之下就能两年解决这个大问题。
陆柱家说,中科院数学与系统科学研究院中由于数论专家很少,而且工作非常繁忙,所以现在对寄来的证明材料无法做到组织专家进行论证。实际上,研究机构并没有这样的权力:即他们自己发表论文。研究机构的研究人员自己的论文也需要向严肃的学术刊物投稿,经过刊物编辑部约请专家审稿之后,如果论文在学术上有意义,并且是正确的,刊物才能录用这篇稿子。陆很坦率地说,希望这些业余研究者能把更多的时间投入到自己的本职工作中去。
陆柱家对记者说,要想证明猜想,其实对其他的研究课题也一样,起码要具备两个基本条件。一是要有数学方面的基本训练,一般来说,必须是数学方面的研究生毕业之后继续从事数学研究工作。陆特别说明一点,在业余研究者中,几乎没有人是学数学出身的。另一方面就是对哥德巴赫猜想这方面的文献有相当的了解。数学家王元在1956年证明“3+4”之前,就查阅过英文、俄文、德文、意大利文等相关文献。
对于某些人以年轻时的华罗庚为例证明业余研究者也能成气候的说法,陆加以了澄清:“华罗庚虽然是业余出身,但自从被熊庆来看中进入清华大学(1931年)之后,就完全是受正规训练了,他当时在清华大学听课和到英国剑桥大学访问(1936年至1938年)。而他的成就都是在受到正规训练后取得的。”
陆说:“两三百年前处于科学的初创阶段,很多在数学研究方面取得成果的人并不是专业数学家,例如,大家所知道的费马大定理的费马(1601—1665)是位律师,他在数学上确实取得了不少成就。但现在情况已经不同,没有一定的数学修养,根本无法攻克这一难题,甚或做一般的研究。”
迄今没有任何人的论证材料得到权威部门认定
记者问道:“会不会漏掉一些确实有价值的证明?”得到的回答是“不可能。”陆柱家研究员说,有些寄来的材料只有一两页,他们可以很快看出证明的破绽,而有些长的一看就知道其入门办法基本一样,“正如我前面所说的,他们把后半部的证明忽略了。”陆说,一些长的材料达到几十页。
迄今为止,没有任何一个人的论证材料得到中科院数学与系统科学研究院的肯定。数学与系统科学研究院的这种做法自然引起了一些“民间数学家”的不满,有人甚至在报章上撰文认为这种做法是“学霸作风”,但陆柱家对此不以为然。他坚持自己的观点:哥德巴赫猜想是一个艰深的数论难题,证明它所需要的扎实的数学能力和突出的思维能力,都并非普通数学爱好者所能企及。
陆柱家认为,如果一些业余研究者在提高了自己的数学修养之后先研究一些其他数学问题,作为研究哥德巴赫猜想的前奏,恐怕更好一些。
在陈景润之后,数学界仍然在继续着哥德巴赫猜想的证明工作,使人们有足够理由相信没有什么问题不能最终解决的是著名的费马大定理的证明。这个定理存在了350多年没人破解,但最终还是于1998年被一个腼腆的英国数学天才安德鲁·威尔斯所证明。终会有一天,哥德巴赫猜想也将不再是一个谜。(鲍丹禾)
1742年6月7日,德国数学家哥德巴赫在写给著名数学家欧拉的一封信中,提出了两个大胆的猜想:一、任何不小于6的偶数,都是两个奇素数之和;二、任何不小于9的奇数,都是三个奇素数之和。这就是数学史上著名的“哥德巴赫猜想”。同年6月30日,欧拉在给哥德巴赫的回信中,明确表示他深信哥德巴赫的这两个猜想都是正确的定理,但是欧拉当时还无法给出证明。
1900年,20世纪最伟大的数学家希尔伯特在国际数学会议上把“哥德巴赫猜想”列为23个数学难题中第8个问题中的一部分。此后20世纪的数学家们在世界范围内“联手”进攻“哥德巴赫猜想”堡垒,终于取得辉煌成果。
1956年,我国数学家王元证明了“3+4”;1957年,他又证明了“3+3”和“2+3”;1962年,我国数学家潘承洞证明了“1+5”;同年又和王元分别证明了“1+4”;1966年,陈景润攻克了“1+2”,也就是:“任何一个足够大的偶数,都可以表示为一个素数及一个不超过二个素数的乘积之和”。这一定理被称为“陈氏定理”。