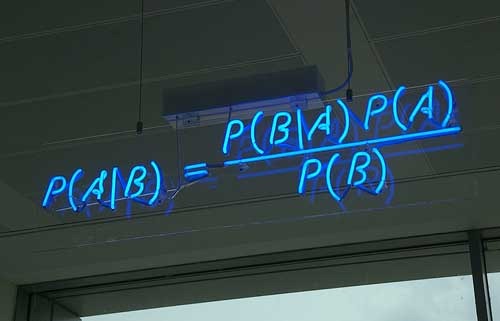如何通俗地解释贝叶斯线性回归的基本原理?

2018-01-07

字体:

大中小

浏览:

文章简介：并不仅仅加了先验p(w), 有很大的区别. 任何的一个基础模型都可以演变成贝叶斯模型.在一个基础模型之下我们需要去estimate一些未知的参数(比如在line

并不仅仅加了先验p(w), 有很大的区别。任何的一个基础模型都可以演变成贝叶斯模型。在一个基础模型之下我们需要去estimate一些未知的参数(比如在linear regression, 需要去计算W这个向量), 但在贝叶斯模型下我们需要去计算的是W的分布(而不是W的point …显示全部

并不仅仅加了先验p(w), 有很大的区别。任何的一个基础模型都可以演变成贝叶斯模型。在一个基础模型之下我们需要去estimate一些未知的参数(比如在linear regression, 需要去计算W这个向量), 但在贝叶斯模型下我们需要去计算的是W的分布(而不是W的point estimation),用其分布直接计算对y的预测值p(y

x,D),所以我们需要去需要integrate W,也就是说我们把所有可能的W向量都会去考虑, 这也为什么贝叶斯模型通常intractable, 所以我们需要用MCMC或者variational方法,而不是直接用优化的方法。在贝叶斯模型之下, 随着我们observe more and more data , 我们会对W向量的分布会有更清晰的推断,这其实就是posterior inference.

下面简单说一下一些预测模型之间的联系:

我们一般考虑3种预测模式,Maximum likelihood estimation (ML), Maximum a posteriori estimation(MAP), 贝叶斯模型. 前两者属于point estimation.

Maximum likelihood estimation (ML): 这是最简单的point estimation, 也就是我们需要去计算P(D

W), 从而找到最优化的W. 它的缺点就是数据比较少的时候往往overfit。

Maximum a posteriori estimation (MAP). 他是在ML的基础上加了prior, 也就是假定了一些P(W)的分布。在MAP情况下我们需要计算P(W

D) (从贝叶斯定理,我们可以得到 P(W

D) \prop P(W) \times P(D

W)). 在linear regression上加上prior其实相当于加了regularization. 如果我们假定P(W)服从高斯分布,那我们加的实际上是L2_norm, 如果我们假定P(W)是拉普拉斯分布,那我们加的是L1_norm(linear regression情况下就是相当于LASSO,会有sparse的特点)。

但是即使regularization会防止overfitting, 但我们还是需要设置regularization coefficient \lamda (比如 minimize \sum_i (y_i-f(_ix,w))^2 \lamda

_2^2). lamda的设置一般需要用cross validation,或者用一些统计学的方法(尽管实际上没有多少人用这个), 所以在MAP的情况下设置这些regularization coefficient成了难题。