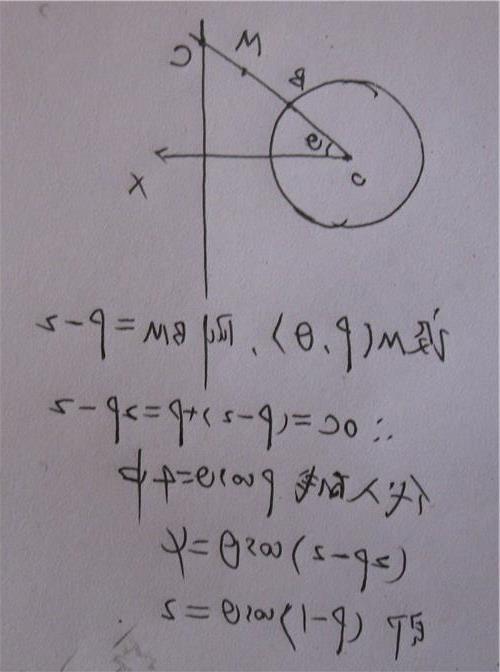笛卡尔坐标如何转换球面坐标 或相互转换
俺理解哈,这是2个3维坐标系之间的一种转换方式【单向的,只能从笛卡尔到直角】。2个坐标系都是一般的3维空间直角坐标系。那3个数字就是空间的1点的3个坐标。
比如,493 ,454, 967是空间中某点在笛卡尔坐标系下的3个坐标。
X=493,Y=454,Z=967.
同样的这个点,在直角坐标系中的3个坐标为16, 13, 22。x=16,y=13,z=22.
同样的这个点在不同坐标系的坐标之间的对应关系是,
x=X的各位数字之和,y=Y的各位数字之和,z=Z的各位数字之和。
X,Y,Z肯定不是凭空来的,是根据笛卡尔坐标系的原点,X,Y,Z轴正向上的单位向量算出来的。换句话说,设定了笛卡尔坐标系以后,空间中的任何点就都有了相对应的笛卡尔坐标了。
【就把这个笛卡尔坐标系理解为游戏里的3维场景所在的1个3维空间坐标系就行了吧。】
X,Y,Z有了以后,就可以转换出x,y,z了。也就是知道了1个点的笛卡尔坐标以后,就可以得到对应的唯一的直角坐标了。
【这个直角坐标系可以理解为游戏里的异空间。但它也是1个3维空间。】
在游戏里,房间是按照某种规律运动的。
但这个规律是关于异空间的【关于直角坐标系的】。
在异空间里,房间按照一定的速度,从1个点移动到另1个点。
3次移动为1个周期。
第1次移动的速度是房间的3个笛卡尔坐标的百位数字 - 十位数字。
第2次移动的速度是房间的3个笛卡尔坐标的十位数字 - 个位数字。
第3次移动的速度是房间的3个笛卡尔坐标的个位数字 - 百位数字。
【哈,如果某个房间的3个坐标的百位=十位=个位。这个房间就永远不会动了。
比如(111,222,333)这样的房间,会静止在那。。】
如果你知道了房间在某个时刻的笛卡尔坐标,你就可以推算出下一个时刻这个房间的直角坐标。然后根据直角坐标可以得到这个房间在笛卡尔坐标系中的可能的几个位置坐标。
比如,现在房间在笛卡尔坐标系下的位置坐标为(477, 804, 539),根据你说的算法,在异空间里【也就是直角坐标系里】,第1次移动,房间会从(4+7+7,8+0+4,5+3+9)=(18,12,17)按照速度(4-7,8-0,5-3)=(-3,8,2)移动到(18,12,17)+(-3,8,2)= (15,20,19)。
第2次移动,房间会从(15,20,19)按照速度(7-7,0-4,3-9)=(0,-4,-6)移动到(15,20,19)+(0,-4,-6)=(15,16,13)。
第3次移动,房间会从(15,16,13)按照速度(7-4,4-8,9-5)=(3,-4,4)移动到(15,16,13)+(3,-4,4)= (18,12,17).
【看到了吧,在异空间里,3次移动后,房间又回到了原位。
因为3次移动的速度之和的3个分量都=百位-十位+十位-个位+个位-百位=0】
俺不能肯定的是,异空间【直角坐标系】里的1个点,是否对应着游戏的3维场景【笛卡尔坐标系】里的唯一的1个点。如果是的话,房间经过3次移动在游戏的3维场景中,也回到了原处。
如果是的话,从直角坐标系到笛卡尔坐标系也应该有1种算法。如果不是的话,那就比较复杂了。即使房间在异空间里回到了原处,它也可能跑到了游戏的场景空间里的另外1个位置了。比如从(477,804,539)跑到了(747,408,359)之类的地方去了。