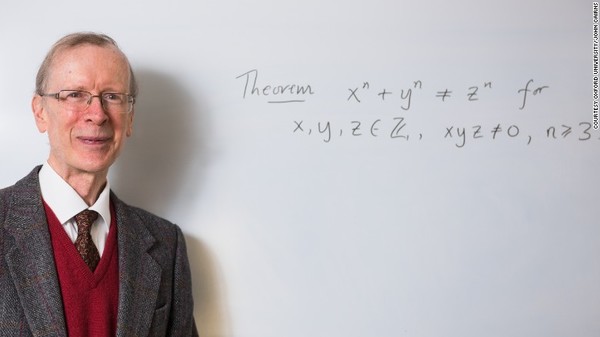费马大定理怀尔斯从3到n:费马大定理得证历程

2017-12-11

字体:

大中小

浏览:

文章简介：[新朋友]点击标题上面蓝色字"老符数学工坊"关注.[老朋友]点击右上角"-"分享到朋友圈公元前500年前后,古希腊毕达哥拉斯学派宰杀百牛欢宴,庆祝毕达哥拉斯定理

【新朋友】点击标题上面蓝色字“老符数学工坊”关注。

【老朋友】点击右上角“…”分享到朋友圈

公元前500年前后,古希腊毕达哥拉斯学派宰杀百牛欢宴,庆祝毕达哥拉斯定理的发现:直角三角形两直角边平方之和等于斜边平方,即x2 y2=z2。公元前12世纪我国《周髀算经》也提出过“勾三股四弦五”,后称勾股定理。如果把幂次提高,对于方程x3 y3=z3直至xn yn=zn能否找到正整数解?这一问题的提出和“解答”始于法国业余数学家费马。

费马贡献最大的领域是数论,但他从不公布,过世后其子才将成果整理出版。大约1637年,费马在阅读古希腊数学家丢番图《算术》第二卷第八命题有关x2 y2=z2的讨论时写道:“将一个立方数分为两个立方数,一个四次幂分为两个四次幂,或者一般地将高于二次的幂分为两个同次的幂,这是不可能的。

关于此,我确信已发现一种奇妙的证法,可惜这里的空白地方太小,写不下。”此话发表于1670年,费马已过世5年。大家翻遍费马遗稿,也没找到这一证明。19世纪初,费马遗留的其他问题均告解决,只剩这一问题悬而未解,是以被称为“费马最后定理”(我国称“费马大定理”)。

1676年数学家根据费马的少量提示用无穷递降法证明了n=4。1678年和1738年德国数学家莱布尼兹和瑞士数学家欧拉也各自证明了n=4。1770年欧拉证明n=3。1823年和1825年法国数学家勒让德和德国数学家狄利克雷先后证明n=5。

1832年狄利克雷试图证明n=7,却只证明了n=14。1839年法国数学家拉梅证明了n=7,随后得到法国数学家勒贝格的简化……19世纪贡献最大的是德国数学家库麦尔,他从1844年起花费20多年时间,创立了理想数理论,为代数数论奠下基础;库麦尔证明当n<> 为推进费马大定理的证明,布鲁塞尔和巴黎科学院数次设奖。

1908年德国数学家佛尔夫斯克尔临终在哥廷根皇家科学会悬赏10万马克,并充分考虑到证明的艰巨性,将期限定为100年。数学迷们对此趋之若鹜,纷纷把“证明”寄给数学家,期望凭短短几页初等变换夺取桂冠。德国数学家兰道印制了一批明信片由学生填写,上面印着:

在解决问题的过程中,数学家们不但利用了广博精深的数学知识,还创造了许多新理论新方法,对数学发展的贡献难以估量。1900年,希尔伯特提出尚未解决的23个问题时虽未将费马大定理列入,却把它作为一个在解决中不断产生新理论新方法的典型例证。

据说希尔伯特还宣称自己能够证明,但他认为问题一旦解决,有益的副产品将不再产生。“我应更加注意,不要杀掉这只经常为我们生出金蛋的母鸡。” 数学家就是这样缓慢而执着地向前迈进,直至1955年证明了n<><><> 1983年,年仅29岁的德国数学家法尔廷斯证明了代数几何中的莫德尔猜想,为此在第20届国际数学家大会上荣获菲尔茨奖;此奖相当于数学界的诺贝尔奖,只授予40岁以下的青年数学家。