数理化 圆周率π的精确值

圆周率π的精确值历史上一个国家所算得的圆周率的准确程度,可以作为衡量这个国家当时数学发展水平的指标。——德国数学史家康托
在古代,圆一直被认为是世界上最简单最完美的形状,以至直到发现开普勒第一定律之前,人们普遍认为行星以及所有天体的运行轨迹是标准圆周,尽管有些科学家也推算出行星的运行轨道与标准圆周不相符,固有的思维定势也要将他们的计算往标准圆周上引。这足以见证古人对圆的偏爱。
圆形是如此完美,如此地招人喜爱,可是要准确计算它的周长和面积却是一件烦恼的事。不过细心的人们很早就发现,无论圆的面积怎样变化,它的周长和直径的比总是保持不变,这个不变的比率就是困惑人们几千年的圆周率。从有文字记载开始,作为一个非常重要的常数,圆周率的精确值一直是许多学者既感兴趣又迫切想要解决的问题,毕竟它在生产生活中的用途太大了。

为了求圆周率的精确值,几千年来,古今中外的数学家们为此耗费了大量的心血。而对π的研究,也在一定程度上反映这个地区或时代的数学水平。正如德国数学史家康托所说:“历史上一个国家所算得的圆周率的准确程度,可以作为衡量这个国家当时数学发展水平的指标。”直到19世纪初,求圆周率的值应该说是数学中的头号难题。
在求圆周率的精确值上,中国在相当长的时间内一直遥遥领先,这也从一个侧面反映古代中国的数学在很多方面处于世界领先水平。
早在公元前1世纪的一部数学著作《周髀算经》里,就有“周三径一”的记载,这其实就是把圆周率当作3。

我国古代木工师傅曾流传这样一句口诀:“周三径一,方五斜七”,其意说,直径为1的圆,周长大约是3,边长为5的正方形,对角线之长约为7。到了东汉时,官方明文规定圆周率取3为计算面积的标准。后人一般将圆周率为3称为“古率”。
在中国应用“古率”之前,古埃及、古希腊已得到了较精确的圆周率,如古埃及取π=4(8/9)2=3.1605;而早在公元前6世纪印度就曾取π=√10=3.162。
求圆周率的更精确近似值的方法最早是阿基米德提出的,他首先用几何方法证明“圆周长与圆直径之比小于3+(1/7)而大于3+(10/71)”。随后在公元150年左右,托勒密求得π=3.1416。此后,直到1427年外国数学家对圆周率的研究再也没有超过小数点后4位数。
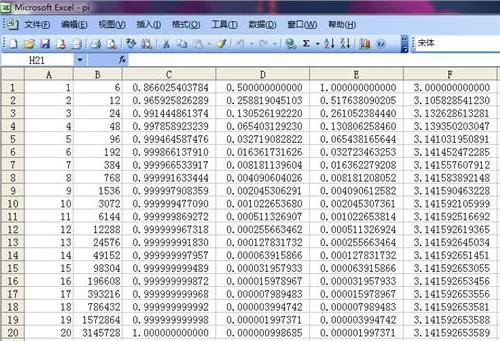
在这一阶段,中国落后了。中国直到公元263年前后,才由刘徽提出著名的割圆术,得出π=3.1416,即“徽率”。不过他的割圆术虽然比阿基米德提出的晚,但其方法要简洁得多,据说他从圆的正192边形开始,一直推算到内接正3072边形才得出这一精确值。
刘徽的割圆术打开了精确求圆周率的方便之门。到了公元5世纪,我国古代著名的数学巨星祖冲之对圆周率的值作出了杰出的贡献,他求得圆周率
3.1415926