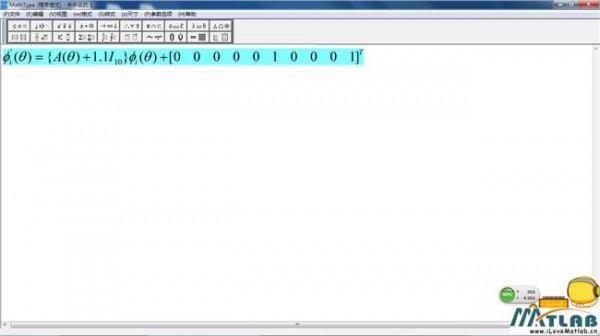
李雅普诺夫函数的构造及应用
20 11 11 Nov. 20 11 年 月 榆林学院学报 21 6 JOURNAL OF YULIN UNIVERSITY Vol. 21 No. 6 第 卷 第 期 李雅普诺夫函数的构造及应用 , 张永华 苑文法 , 7 10055 西安建筑科技大学理学院 陕西西安 : , , 摘 要 运用李雅普诺夫稳定性理论对系统零解稳定性判断分析 介绍了函数的构造方法和形式 并举 例说明。
: ; ; 关键词 李雅普诺夫定理 稳定性 李雅普诺夫函数 中图分类号:O29 文献标志码:A 文章编号:1008 - 387 1 20 11 06 - 0021 - 03 , 1 李雅普诺夫是稳定性理论的创始人 稳定性理 τ ; V t ,x x x 平面上为常正函数 函数 2 是半正 论是分析和研究非线性控制系统稳定性的经典理 1 t , 。
定的但不是正定的。 论 现在仍被大家广泛采用 处理稳定性问题有两 。
, 。 定义2 V x ,y 在相空间坐标原点的邻域 D 种方法 其中 第二种方法比较常用 其借助李雅 , , dV 中连续可微 把函数称为关于系统的全导数 记为 普诺夫函数和微分方程所计算出来的导数 的符 dt dV dV dx1 dV dx2 dV dxn n dVdxi … ∑ , 。
dt dx dt dx dt dx dt i 1dx dt 号性质 就能直接推断出解的稳定性 李雅普诺夫 1 2 n i , 1 理论的核心是构造一个李雅普诺夫函数 学者们已 定理 如果对于动力学方程存在一个李雅普 经提出了一些构造非线性系统李雅普诺夫函数的方 dV 诺夫函数V x , D 其全导数 是负半定的 即对于 dt , , 、 , 法 比如 克拉索夫斯基法 变量梯度法等 但每种方 ・ V x 0 , 。
中所有点 ≤ 则方程的定点是稳定的 , 法都有其一定的针对性 还没有一个能适用于各种 2 定理 如果对于方程存在一个李雅普诺夫函数 。 , 情况的统一构造方法 本文通过实例分析 针对性 dV ・ 的给出了李雅普诺夫函数的一些构造方法