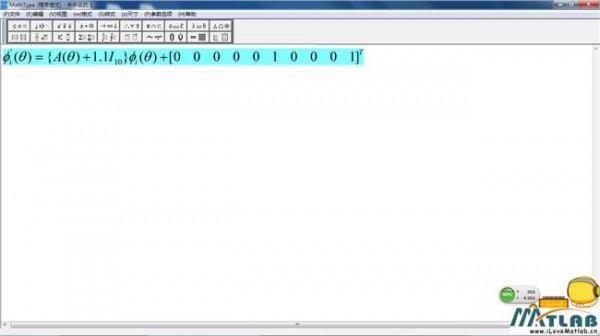
李雅普诺夫俄文 关于李雅普诺夫全局稳定性证明的讨论?
大家 @戎佩琰@Kaixiang Wang 已经回答了这个问题了,我说一下我的答案: 首先统一说法,这个题设中只有原点这一个平衡点 ,即(x1=0,x2=0),系统是二阶系统,x1和x2只是系统的两个状态。
一: 1.是 2.是 二: 1.是 2.不对。 3.不可以。在你的具体问题中,只能说系统的两个状态最后会收敛到零点附近的一个区域内,而不能认定其中任何一个状态变为0. 4.是一个概念。全局渐进稳定就是大范围渐进稳定。
5.V(x)必须包括所有状态。 在此之外补充一些: 全局稳定性是很难证明的。如果系统要有全局稳定,有一个大前提就是系统要有至少一个稳定的平衡点。 再说一下李雅普诺夫下的稳定性。
稳定性这个东西有很多种定义,比如输入输出有界稳定,指数稳定,好像有人说过稳定性的定义有二十多种。这里只说在李雅普诺夫下的三种定义: 1.稳定。在一个区域内,有能量函数V(x)>0,且能量函数的导数小于等于0。
在这种情况下,物理上的解释可以说为,系统的能量不总是耗散的,有可能在到达平衡点之前能量就保持不变了,这时候是不能说系统状态一定会收敛到平衡点的,只能保证收敛到平衡点附近的一个邻域。 2.
渐进稳定(范围内渐进稳定)。在一个区域内,有能量函数V(x)>0,且能量函数的导数小于0。这时候在这个区域内,是能保证收敛到平衡点的。 3.全局渐进稳定(大范围内渐进稳定)。如果x趋向于无穷,V(x)也趋向于无穷,且V(x)的导数小于0,这时候系统是全局渐进稳定的,不论什么初始条件下,总能收敛到平衡点。
这是一个在构造能量函数的时候容易忽略的地方,即构造的V(x)虽然正定,但是不满足上述条件,从而达不到全局稳定,而只能在一定区间内稳定。 还有系统有多个独立平衡点的位置,及时李雅普诺夫定理证明了全局稳定性,但也不能证明系统最后会收敛到哪个平衡点上,只能知道会收敛到某个稳定平衡点上