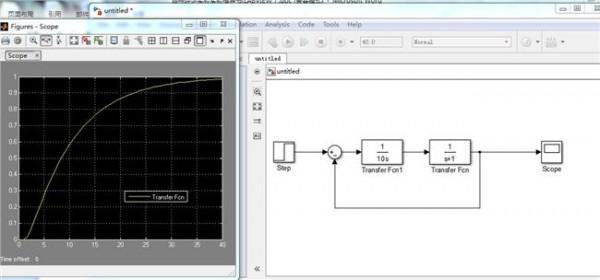
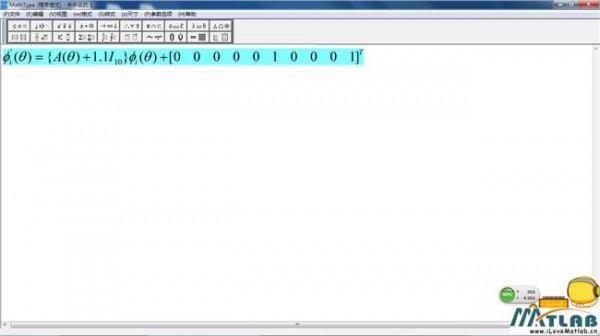
李雅普诺夫讲解 基于MATLAB的李雅普诺夫第二法稳定性分析
基于MATLAB的李雅普诺夫第二法稳定性分析
引言:对于一个给定的控制系统,稳定性是系统的一个重要特性。稳定性是系统正常工作的前提,是系统的一个动态属性。在控制理论工程中,无论是调节器理论、观测器理论还是滤波预测、自适应理,都不可避免地要遇到系统稳定性问题,而且稳定性分析的复杂程度也在急剧增长。
当已知一个系统的传递函数或状态空间表达式时, 可以对其系统的稳定性进行分析;当系统的阶次较高时,分析、计算的工作量很大, 给系统的分析带来很大困难。运用MATLAB 软件,其强大的科学计算能力和可视化编程功能, 为控制系统稳定性分析提供了强有力的工具。
一. MATLAB 语言简介
MATLAB 是MATrix LABoratory 的缩写, 它是MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。
它具有强大的矩阵计算能力和良好的图形可视化功能, 为用户提供了非常直观和简洁的程序开发环境, 因此被称为第四代计算机语言。MATLAB 发展至今, 现已集成了许多工具箱, 一般来说, 它们都是由特定领域的专家开发的, 用户可以直接是用工具箱学习、应用和评估不同的方法而不需要自己编写代码,大大提高了分析运算的效率,为此MATLAB 语言在控制工程领域已获得了广泛地应用。
二.控制系统稳定性的基本概念
稳定性是控制系统的重要特性, 也是系统能够正常运行的首要条件。如何分析系统的稳定性并提出保证系统稳定的措施, 是自动控制理论的基本任务之一。1892年,俄国数学家李雅普诺夫(Lyaponov)提出了分析稳定性的两种方法。
第一种方法,通过对线性化系统特征方程的根的分析情况来判断稳定性,称为间接法。此时,非线性系统必须先线性近似,而且只能使用于平衡状态附近。第二种方法,从能量的观点对系统的稳定性进行研究,称为直接法,对线性、非线性系统都适用。
Lyaponov定义下的稳定性,是对任何系统都适用的关于稳定性的一般性定义。系统平衡态问题就是:偏离系统平衡态的受扰运动能否仅依靠系统内部的结构因素,就能使系统返回到初始平衡,或者使之限制在平衡态的有限邻域内。
三.Lyaponov第二法的稳定性判据
3.1 在现代控制理论中,李雅普诺夫第二方法是研究稳定性的主要方法,既是研究控制系统理论问题的一种基本工具,又是分析具体控制系统稳定性的一种常用方法。李雅普诺夫第二方法的局限性,是运用时需要有相当的经验和技巧,而且所给出的结论只是系统为稳定或不稳定的充分条件;但在用其他方法无效时,这种方法还能解决一些非线性系统的稳定性问题。
3.1.1 Lyaponov第二法又称直接法,从能量的观点来研究系统的稳定性问题。其基本思想是:系统所具有能量是状态矢量x的标量函数,且平衡状态具有的能量最小。进而通过能量函数V(x)和 的正负判断系统的稳定性。