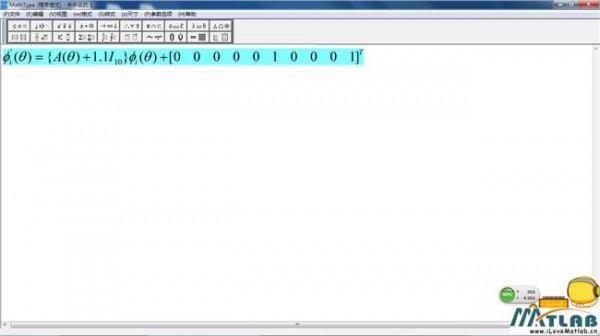
李雅普诺夫定理 李雅普诺夫稳定性理论要点
第三章李雅普诺夫稳定性理论研究的目的和意义:稳定性是自动控制系统正常工作的必要条件,是一个重要特征。要求:在受到外界扰动后,虽然其原平衡状态被打破,但在扰动消失后,仍然能恢复到原来的平衡状态,或者趋于另一平衡状态继续工作。
稳定性:系统在受到小的外界扰动后,系统状态方程解的收敛性,而与输入作用无关。经典控制理论稳定性判别方法:代数判据,奈魁斯特判据,对数判据,根轨迹判据非线性系统:相平面法(适用于一,二阶非线性系统)1982年,俄国学者李雅普诺夫提出的稳定性定理采用了状态向量来描述,适用于单变量,线性,非线性,定常,时变,多变量等系统。
应用:自适应,最优控制,非线性控制等。主要内容:李氏第一法(间接法):求解特征方程的特征值李氏第二法(直接法):利用经验和技巧来构造李氏函数孤立的平衡状态:在某一平衡状态的充分小的领域内不存在别的平衡状态。
对于孤立的平衡状态,总可以经过适当的坐标变换,把它变换到状态空间的原点。
当与无关大范围一致渐进稳定。必要条件:在整个状态空间中只有一个平衡状态不稳定性:不管,有多小,只要内由出发的轨迹超出以外,则称此平衡状态是不稳定的。线性系统的平衡状态不稳定表征系统不稳定。
非线性系统的平衡状态不稳定只说明存在局发散的轨迹。至于是否趋于无穷远域外是否存在其它平衡状态。若存在极限环,则系统仍是李雅普诺夫意义下的稳定性。非线性系统的稳定性分析:假定非线性系统在平衡状态附近可展开成台劳级数,可用线性化系统的特征值判据判断非线性系统的平衡状态处的稳定性。
设非线性系统状态方程:在平衡状态附近存在各阶偏导数,于是:上式为向量函数的雅可比矩阵。令则线性化系统方程为:结论:若,则非线性系统在处是渐进稳定的,与无关。
若则不稳定。若,稳定性与有关,则是李雅普诺夫意义下的稳定性。3.4李雅普诺夫第二法(直接法)稳定性定理:设系统状态方程:其平衡状态满足,假定状态空间原点作为平衡状态(),并设在原点领域存在对x的连续的一阶偏导数。
定理1:若(1)正定;(2)负定;则原点是渐进稳定的。说明:负定能量随时间连续单调衰减。定理2:若(1)正定;(2)负半定;(3)在非零状态不恒为零,则原点是渐进稳定的。
说明:不存在,经历能量等于恒定,但不维持在该状态。定理3:若(1)正定;(2)负半定;(3)在非零状态存在恒为零;则原点是李雅普诺夫意义下稳定的。说明:系统维持等能量水平运动,使维持在非零状态而不运行至原点。
定理4:若(1)正定;(2)正定则原点是不稳定的。说明:正定能量函数随时间增大,在处发散。线性系统不稳定非线性系统不一定推论1:当正定,正半定,且在非零状态不恒为零时,则原点不稳定。
推论2:正定,正半定,若,,则原点是李雅普诺夫意义下稳定(同定理3)。几点说明:选取不唯一,但没有通用办法,选取不当,会导致不定的结果。这仅仅是充分条件。--单调衰减(实际上是衰减振荡)李氏第二法的步骤:构造一个二次型;求,并代入状态方程;判断的定号性;判断非零情况下,是否为零。
令若成立李氏意义下稳定若仅成立渐进稳定例1:已知非线性系统的状态方程为:试用李雅普诺夫第二法判断其稳定性。解:设则几何意义:例2:试判断下列线性系统平衡状态的稳定性。
解:1)则:例3:试判断下列线性系统平衡状态的稳定性。解:由于设则故系统是李雅普诺夫意义下的稳定。例4:试判断下列线性系统平衡状态的稳定性。解:即设则可见与无关,故非零状态(如)有,而对其余任意状态有故正半定。
令即非零状态时,不恒为零,则原点不稳定即系统不稳定。3.5线性定常系统渐进稳定性判别法设系统状态方程为:为唯一平衡状态。设选取如下的正定二次型函数为李氏函数则:令由渐进稳定性定理1,只要Q正定(即负定),则系统是大范围一致渐进稳定。
定理:系统大范围渐进稳定的充要条件为:给定一正交实对称矩阵Q,存在唯一的正定实对称矩阵P使成立,则为系统的一个李氏函数。
方法1:给定PQV(x)选取不定Q不定。给定正定QPQ单位阵p的定号性方法2:Q取正半定(定理2)允许单位矩阵主对角线上部分元素为零负半定。例1:解:选取线性定常离散系统渐进稳定性判别设系统状态方程:其中-非奇异阵,是平衡状态。
设定理:系统渐进稳定的充要条件为:给定任一正定实对称阵Q,存在一个正实对称P,使式成立,则是系统的一个李氏函数。可取Q=I,如果且Q为正半定阵。负定原点是渐进稳定的;只有一个平衡状态,该系统是大范围渐进稳定;由于V(x)与t无关,又是大范围一致渐进稳定。
定理1等能量轨迹(整个平面)令即原点是平衡状态。设其它负半定令只有全零解非零状态时原点是渐进稳定,且是大范围一致渐进稳定。
定理2则原点是平衡状态定理3推论1--非奇异矩阵将代入:P正定是大范围一致渐进稳定令李氏代数方程**3.1稳定性基本概念3.2李雅普诺夫意义下的稳定性3.3李雅普诺夫第一法3.4