郎之万的一生 与居里夫人不得不说的故事

保罗·朗之万(Paul Langevin，1872.1.23~1946.12.19)法国物理学家。主要贡献有朗之万动力学及朗之万方程。 Langevin在民国时期的资料中常译为郎之万  ，但现今台湾也有译为"朗"的。郎之万为法共党员。强烈反对纳粹，因而在维希政府时期声望大受影响，但法国光复后声望得到恢复。1931年来过中国考察，对中国抗战抱支持态度。

中  文  名：保罗·朗之万

外  文  名：Paul Langevin

国       籍：法国

出  生  地：巴黎

出生日期：1872年1月23日

逝世日期：1946年12月19日

职       业：物理学家

毕业院校：剑桥大学，法兰西学院，巴黎大学

1872年1月23日生于巴黎，逝世于1946年12月19日。他是反法西斯知识分子警觉委员会的创始人之一，该委员会是一个尾随1934年2月6日极右暴乱成立的反法西斯组织。他曾于1944年至1946年任法国人权联盟主席(当时他刚加入了法国共产党)。

朗之万出生于巴黎，曾就读于巴黎市立高等工业物理化学学校及巴黎高等师范学校。1897年毕业后，他来到剑桥大学，在约瑟夫·汤姆孙的指导下于卡文迪许实验室学习。后来，朗之万回到巴黎大学，并在皮埃尔·居里的指导下于1902年取得博士学位。1904年，朗之万成为法兰西学院的物理学教授。1926年成为巴黎市立高等工业物理化学学校主任。1909年任法兰西学院教授，1934年当选为法兰西科学院院士，1930年和1933年曾两度当选为索尔维物理学会议主席。1934年入选法国科学院。1911年，朗之万与居里夫人之间的风流韵事在巴黎甚嚣尘上。他以直言不讳反对纳粹主义著称，纳粹德国占领法国时，他被维希政府革职，1944年方恢复原职。朗之万在巴黎解放两年后的1946年逝世。

居里夫人给郎之万的一封信中是这样描述她对两人关系的看法的：“我们两人极有缘分，只要有一小块肥沃的土地，便能发展出来。过去我们有时也感到此点，可是直到我在悲叹自己塑造的人生时，我俩面对面单独相处，才充分体会到这一事实。那时你也才找到在你家里完全找不到的感觉。”郎之万不能忍受和子女分离，他迟疑不决时，玛丽写道：“把我们俩拉合在一起的是一种强烈的本能。你觉不觉得，毁灭一份真挚而深刻的感情，像是令自己珍爱的孩子死去一般？我们眼看着那份感情滋长，有时候毁掉它比失去孩子更加不幸，不是吗？”

“玛丽显然不怕写下她的感情。她写道：‘万事万物，不都是从这样的感情来的吗？我认为这是我们所有一切的根源——和谐的工作关系、密切坚贞的友谊、生活的勇气，甚至最美的爱情’。”还有一段值得收入女性书信选集，也更说明了玛丽·居里的个性：“你首先要做的是回到自己的卧室。我答应不再责难你，你可以相信我。我完全信任你的意向，可是我担心无法预见的事情——例如对方号啕大哭，令你无可抗拒；或用诡计让你使她在怀孕。如果她再怀孩子，我们就一定要分手了，因为我不能接受这份耻辱。你的妻子若明白这一点，一定会加以利用。所以我求你别再睡在她的床上，不要让我等太久了。”

朗之万以对次级X射线、气体中离子的性质、气体分子动理论、磁性理论以及相对论方面的工作著称。朗之万以其对顺磁性及抗磁性的研究而闻名，他提出用现代的原子中的电子电荷去解释这些现象。他最著名的研究是使用皮埃尔·居里的压电效应的紫外线应用。第一次世界大战期间，为了探测潜艇，利用石英的压电振动获得了水中的超声波，他开始用声波去探测潜艇并以其回音确定其位置的研究。但装置能运作时，大战已经结束。在他的研究生涯中，在法国做出很多传播相对论的工作。

1905年提出关于磁性的理论，用基元磁体的概念对物质的顺磁性及抗磁性作了经典的说明。1908年发展了布朗运动的涨落理论。同时，他坚决反对法西斯，反对侵略，在第二次世界大战期间，曾被德国占领军逮捕入狱，和法西斯进行了严正的斗争。中国九一八事变后，他进行了各种声援中国的活动，并批评了国际联盟对日本侵略者的纵容。

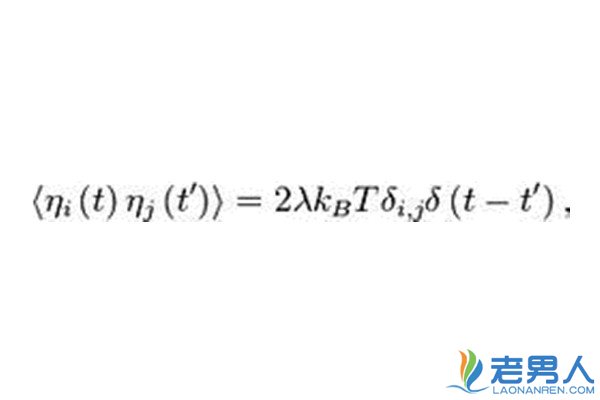
原朗之万方程描述了布朗运动由于流体的分子的碰撞，粒子在流体中做无规则运动这里，自由度是粒子的位置x，m表示粒子的质量。作用在粒子上的力写成正比于粒子的速度（斯托克斯定律）的粘滞力，和一个表示流体分子碰撞影响的噪声项η(t)的和。其中kB是波耳兹曼常数和T是温度。

该δ函数在时间上的相关性形式表示在时间t上的力,其被假定为在任何其他时间里完全不与它相关。这是一个近似值; 实际的随机力具有对应于分子碰撞时间的非零相关时间。然而，朗之万方程是用来描述在一个更长时间刻度上“宏观”粒子的运动，并在此极限上的δ-相关和朗之万方程变得精确。 朗之万方程的另一个典型特征是随机力的相关函数中衰减系数λ的出现，这一事实也被称为爱因斯坦关系。