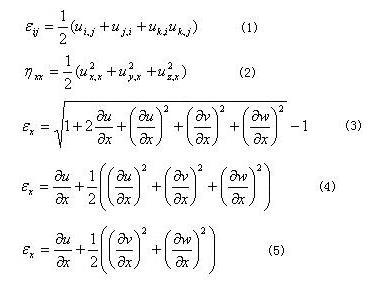【张量分解】cp分解和tucker分解张量分解基础

2018-03-17

字体:

大中小

浏览:

文章简介：张量(tensor)理论是数学的一个分支学科,在力学中有重要应用.张量这一术语起源于力学,它最初是用来表示弹性介质中各点应力状态的,后来张量

张量（tensor）理论是数学的一个分支学科，在力学中有重要应用。张量这一术语起源于力学，它最初是用来表示弹性介质中各点应力状态的，后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要，在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广，矢量是一阶张量。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。

张量（Tensor）是一个定义在的一些向量空间和一些对偶空间的笛卡儿积上的多重线性映射，其坐标是

维空间内，有

个分量的一种量，其中每个分量都是坐标的函数，而在坐标变换时，这些分量也依照某些规则作线性变换。r 称为该张量的秩或阶（与矩阵的秩和阶均无关系）。

在同构的意义下，第零阶张量（r = 0）为标量（Scalar），第一阶张量（r = 1）为向量（Vector），第二阶张量（r = 2）则成为矩阵（Matrix）。例如，对于3维空间，r=1时的张量为此向量：（x,y,z）。

由于变换方式的不同，张量分成协变张量（Covariant Tensor，指标在下者）、逆变张量（Contravariant Tensor，指标在上者）、混合张量（指标在上和指标在下两者都有）三类。

在数学里，张量是一种几何实体，或者说广义上的“数量”。张量概念包括标量、向量和线性算子。张量可以用坐标系统来表达，记作标量的数组，但它是定义为“不依赖于参照系的选择的”。张量在物理和工程学中很重要。例如在扩散张量成像中，表达器官对于水的在各个方向的微分透性的张量可以用来产生大脑的扫描图。

可能最重要的工程上的例子就是应力张量和应变张量了，它们都是二阶张量，对于一般线性材料他们之间的关系由一个四阶弹性张量来决定。

虽然张量可以用分量的多维数组来表示，张量理论存在的意义在于进一步说明把一个数量称为张量的涵义，而不仅仅是说它需要一定数量的有指标索引的分量。特别是，在坐标转换时，张量的分量值遵守一定的变换法则。张量的抽象理论是线性代数分支，现在叫做多重线性代数。

彭毅1基本概念及记号2?张量(tensor)?多维数组一阶张量(向量)三阶张量二阶张量(矩阵)3?张量空间?由若干个向量空间中的基底的外积张成的空间?向量的外积和内积

4?阶(order/ways/modes/rank)

?张成所属张量空间的向量空间的个数

一阶张量(向量):?{xi}x二阶张量(矩阵):?{xij}X三阶或更高阶张量:?{xij?k}X零阶张量(数量):x

三阶张量:X

I×J×K

纤维(fiber)

mode-1(列)纤维:x:jk

mode-2(行)纤维:xi:k

mode-3(管)纤维:xij:

切片(slice)

水平切片:Xi::

侧面切片:X:j:

正面切片:X::k(Xk)

内积和范数

?设X,Y内积:

I1×I2××IN?

X,Y?xi1i2?iNyi1i2?iN

i1?1i2?1iN?1

(Frobenius)范数:

X,X?

xi2i2?iN1

i1?1i2?1iN?1

秩一张量/可合张量

N阶张量XI1×I2××IN是一个秩一张量,如果它能被写成N个向量的外积,即

X?a(1)?a(2)?a(N)

三阶秩一张量:X

?a?b?c

(超)对称和(超)对角

?立方张量:各个mode的长度相等?对称:一个立方张量是对称的,如果其元素在下标的任意排列下是常数。

如一个三阶立方张量是超对称的,如果

xijk?xikj?xjik?xjki?xkij?xkji,?i,j,k?对角:仅当i1?i2?iN时,xi1i2?iN?0

张量的(超)对角线

展开(matricization/unfolding/flattening)

?将N阶张量X沿mode-n展开成一个矩阵X(n)

X?X(1)?

三阶张量的mode-1展开

n-mode(矩阵)乘积

一个张量XI1×I2××IN和一个矩阵UJ×In的n-mode乘积?X?nU?I1×?×In?1×J×In?1×?×IN,其元素定义为I

?X?nU?i?i

n?1jin?1?iN

xi1i2?iNujin

in?1

?这个定义可以写成沿mode-n展开的形式

Y?X?nU?Y(n)?UX(n)

?性质:X?mA?nB?X?nB?mA,m?n

X?nA?nB?X?n?BA?

n-mode(向量)乘积

一个张量XI1×I2××IN和一个向量vIn的n-mode乘积?X?nv?I1×?×In?1×In?1×?×IN,其元素定义为

?X?nv?i?i

n?1in?1?iN

xi1i2?iNvin

in?1

?性质:

X?ma?nbX?man?1bX?nbma,m?n

矩阵的Kronecker乘积

I×J

,BK×L,则

?a11Ba12B?aBaB22A?B21?aI1BaI2B

?a1JBa2JBIK×JL?aIJB?

?性质:?A?BC?D?AC?BD?

?A?B?

?A+?B+

矩阵的Kronecker乘积

?矩阵的Kronecker积还和张量和矩阵的n-mode乘积有如下关系

Y?X?1A(1)NA(N)?Y(n)?AX(n)?A

(n)(N)

(n?1)

(1)T

矩阵的Khatri-Rao乘积

?AI×K,BJ×K,则

A?Ba1?b1a2?b2?aK?bK?IJ×K

?性质:A?B?CA?BC?AB?C?

矩阵的Hadamard乘积

,BI×J?a11b11?abA?B2121aI1bI1

I×J

,则

a12b12a22b22?aI2bI2

?a1Jb1Ja2Jb2JI×J?aIJbIJ?

?性质:?A?B?

?A?B?ATA?BTB?

?A?B?AA?BB?

+TT

?A?B?

CP分解

CP分解的其他名字

?PolyadicFormofaTensor,Hitchcock,1927?PARAFAC(ParallelFactors),Harshman,1970?CANDECOMP/CAND(Canonicaldecomposition),CarrollChang,1970?TopographicComponentsModel,M?cks,1988?CP(CANDECOMP/PARAFAC),Kiers,2000

CP分解的张量形式

?将一个张量表示成有限个秩一张量之和,比如一个三阶张量可以分解为

XA,B,C?ar?br?cr

r?1

三阶张量的CP分解

CP分解的矩阵形式

?因子矩阵:秩一张量中对应的向量组成的矩阵,如

Aa1a2?aR?

?利用因子矩阵,一个三阶张量的CP分解可以写成展开形式

X(1)?A?C?B?

X(2)?B?C?A?X(3)?C?B?A?

CP分解的切片形式

?三阶张量的CP分解有时按(正面)切片写成如下形式:

Xk?AD(k)BT

D(k)?diag(ck:)其中

D(k)

三阶张量CP分解的正面切片形式

带权CP分解

?为了计算方便,通常假设因子矩阵的列是单位长度的,从而需要引入一个权重向量λR,使CP分解变为

Xλ;A,B,Crar?br?cr

?对于高阶张量,有

r?1

Xλ;A(1),A(2),?,A(N)ra(1)?a(2)?a(rN)rr

r?1

其展开形式为

X(n)?Adiag(λ)?A

(n)

(N)

(n?1)

(1)

张量的秩和秩分解

?张量X的秩定义为用秩一张量之和来精确表示X所需要的秩一张量的最少个数,记为rank(X)?秩分解:

rank(X)

r?1

a(1)?a(2)?a(rN)rr

可见秩分解是一个特殊的CP分解,对应于矩阵的SVD?目前还没有方法能够直接求解一个任意给定张量的秩,这被证明是一个NP-hard问题

张量的秩

?不同于矩阵的秩,高阶张量的秩在实数域和复数域上不一定相同。例如一个三阶张量X?1001?X1X2?0110在实数域内进行秩分解得到的因子矩阵为?101101110?A?B011?C?11101?1?而在复数域内进行分解得到的因子矩阵为?11?1?11?1?11?A?ii?Bi?i?Ci?i?2?2?

张量的低秩近似

?相对于矩阵的SVD来说,高阶张量的秩分解唯一性不需要正交性条件保证,只需满足:

n?1

A(n)

?2R?N?1

这里kA表示矩阵A的k-秩:任意k列都线性无关的最大的k

张量的低秩近似

?然而在低秩近似方面,高阶张量的性质比矩阵SVD差

?Kolda给出了一个例子,一个立方张量的最佳秩-1近似并不包括在其最佳秩-2近似中,这说明张量的秩-k近似无法渐进地得到?下面的例子说明,张量的“最佳”秩-k近似甚至不一定存在

X?a1?b1?c2?a1?b2?c1?a2?b1?c1111Y?a1?a2?b1?b2?c1?c2?a1?b1?c1?

张量的低秩近似

?退化:如果一个张量能够被一系列的低秩张量任意逼近?边缘秩(borderrank):能够任意逼近一个张量的最少的成分个数

秩2秩3

(0)

(1)

X(2)

一个秩为2的张量序列收敛到一个秩3张量

CP分解的计算

?分解成多少个秩一张量(成分)之和?

?通常的做法是从1开始尝试,知道碰到一个“好”的结果为止?如果有较强的应用背景和先验信息,可以预先指定

?对于给定的成分数目,怎么求解CP分解?

?目前仍然没有一个完美的解决方案?从效果来看,交替最小二乘(AlternatingLeastSquare)是一类比较有效的算法

CP分解的计算

?以一个三阶张量X为例,假定成分个数R已知,目标为

?minX?X?

?s.

t.X?rar?br?crλ;A,B,C?

r?1

?作为ALS的一个子问题,固定B和C,求解

minX(1)?Adiag(λ)?C?B?

T+

得Adiag(λ)?X(1)C?B?X(1)?C?B?CC?BB

再通过归一化分别求出A和λ

CP分解的计算

?ALS算法并不能保证收敛到一个极小点,甚至不一定能收敛到稳定点,它只能找到一个目标函数不再下降的点?算法的初始化可以是随机的,也可以将因子矩阵初始化为对应展开的奇异向量,如将A初始化为X(1)的前R个左奇异向量

CP分解的应用

?计量心理学语音分析化学计量学独立成分分析神经科学数据挖掘高维算子近似随即偏微分方程…………

Tucker分解

Tucker分解的其他名字

?Three-modefactoranalysis(3MFA/Tucker3),Tucker,1966?Three-modeprincipalcomponentanalysis(3MPCA),KroonenbergDeLeeuw,1980?N-modeprincipalcomponentsanalysis,Kapteynetal.

,1986?Higher-orderSVD(HOSVD),DeLathauweretal.

,2000?N-modeSVD,VasilescuandTerzopoulos,2002

Tucker分解

?Tucker分解是一种高阶的主成分分析,它将一个张量表示成一个核心(core)张量沿每一个mode乘上一个矩阵。对于三阶张量XI×J×K来说,其Tucker分解为

XG;A,B,CG?1A?2B?3Cgpqrap?bq?cr

p?1q?1r?1

?因子矩阵AI×P,BJ×Q,C可以视为沿相应mode的主成分

K×R

通常是正交的,

Tucker分解

?容易看出,CP分解是Tucker分解的一种特殊形式:如果核心张量G是对角的,且P?Q?R,则Tucker分解就退化成了CP分解

G?2B?3CBGGG?1A?2B?A?C

三阶张量的Tucker分解

Tucker分解的矩阵形式

?三阶Tucker分解的展开形式为

X(1)?AG(1)?C?B?

X(2)?BG(2)?C?A?X(3)?CG(3)?B?A?

?Tucker分解可以推广到高阶张量

X?G?1A(1)?2A(2)NA(N)G;A(1),A(2),?,A(N)?

X(n)?AG(n)?A

(n)(N)

(n?1)

(1)

Tucker2和Tucker1

?对于三阶张量固定一个因子矩阵为单位阵,就得到Tucker分解一个重要的特例:Tucker2。

例如固定C?I,则

X?G?1A?2BG;A,B,I?

?进一步,固定两个因子矩阵,就得到了Tucker1,例如令第二、三个因子矩阵为单位阵,则Tucker分解就退化成了普通的PCA

X?G?1AG;A,I,IX(1)?AG(1)

张量的n-秩近似

?一个N阶张量X的n-秩定义为

rankn(X)?rank(X(n))

?若设rankn(X)?Rn,n?1,?,N,则X叫做一个秩?R1,R2,?,RN?张量?如果rankn(X)?Rn,n?1,?,N,则很容易得到X的一个精确秩-?R1,R2,?,RN?Tucker分解;然而如果至少有一个n使得rankn(X)?Rn,则通过Tucker分解得到的就是X的一个秩-?R1,R2,?,RN?近似

张量的n-秩近似

rank1(X)

截断的Tucker分解:秩-

?R1,R2,R3?近似

张量的n-秩近似

?对于固定的n-秩,Tucker分解的唯一性不能保证,所以需要添加其他的约束?通常要求核心张量是“简单”的,如各个mode的主成分之间尽量不发生相互作用(稀疏性),或者其他的“简单性”约束

Tucker分解的计算

?HOSVD:利用SVD对每个mode做一次Tucker1分解(截断或者不截断)?HOSVD不能保证得到一个较好的近似,但HOSVD的结果可以作为一个其他迭代算法(如HOOI)的很好的初始解

Tucker分解的计算

?为了导出HOOI迭代算法,先考虑目标函数

G;A(1),?,A(N)?

?vec(X)A(N)?A(1)?vec(G)