朴素贝叶斯分类及应用
贝叶斯学习器其实是从经典的贝叶斯概率公式的来的,对于经典的贝叶斯公式:
P(A
B)=P(B
A)P(A)P(B)
式中P(A)表示A的先验概率(即A发生的概率与B无关),P(A
B)表示A的后验概率(即在已知B发生的情况下,A发生的概率)
我们都知道贝叶斯是一个经典的求取概率的公式,那么贝叶斯又是怎么和分类相联系起来的呢?
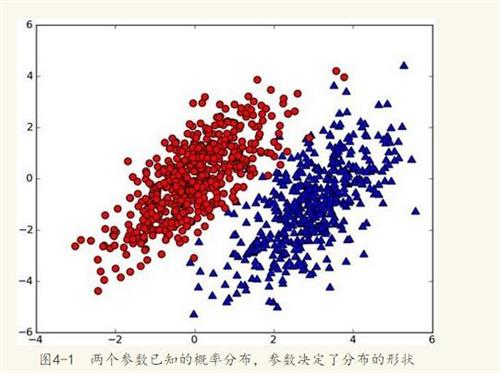
实际上,在分类的过程中,我们要判断某样本x是否属于某类别A时,可以将这件事看成是个概率问题,即判断x属于A的可能性有多大。假设类别有n种,则只需求取x分别属于每个样本的概率有多大,概率值最大的,即可认为是x的所属类别。
朴素贝叶斯分类的正式定义如下:
1. 设x={a1,a2,...,am}为一个带分类项,其中每个a的为x的一个特征属性.
2. 有类别集合$C={y1,y2,...yn}$。
现在从定义可以看出每步并不难理解。关键时第三步中的每个概率值怎么求取。对于单个变量,求取其概率值比较好求,可是这里的x时一个含有m个属性的变量,这种情况下,该怎么求取其属于某类别yn的概率是多少呢?
下面给出求解推导:
已知我们要求取P(yi
x)的概率值,根据贝叶斯公式可以将其转换为如下形式:
P(yi
x)=P(x
yi)P(yi)P(x)
所以求取P(yi
x)就变成了求P(x
yi)P(yi)P(x)。
对于P(x
yi),因为x含有m个属性变量,因此可以将其写成P({a1,am}
yi)。对于大多数情况,x的各个属性之间都是相互独立,所以有:
yi)P(yi)=P(a1
yi)P(a2
yi)...P(am
yi)P(yi)=P(yi)∏j=1mP(aj
P(yi
x)=P(yi)∏mj=1P(aj
yi)P(x)
至此,便得到了P(yi
x)的概率值求解表达式,不过这里的P(X)的值不知道为多少。但是,根据贝叶斯分类的思想,我们只要找到概率最大的一项即即可,对于不同的类别yi,P(yi
x)最终的求解表达式中都含有P(X),因此只要求解,使P(yi)∏mj=1P(aj
yi)最大即可。
对于目标跟踪,目前用的比较多的方法都是在待跟踪目标区域周围获取候选窗口,然后判断这些候选窗口是否是目标。在判断的过程中,往往采都是计算候选窗口属于时目标的概率值,值越大,则其时目标的可能性就越大。这种思想和朴素贝叶斯分类的思想非常相似。
下面以压缩感知跟踪为例。
在感知压缩跟踪,作者将贝叶斯当成了一个在线学习的分类器,此分类器在分为分类和更新参数两个部分。
首先在目标框(t-1帧确定的位置)周围一定范围内选取m个候选框。对候选框提取特征,得到特征向量v? =(v1,v2,vn)每个向量都含有n个属性值,现要求v? 是后选框的概率值,根据朴素贝叶斯可知:
P(y=1
v? )=P(y=1)∏ni=1P(vj
y=1)P(v? )
但是要是单纯的求取这个式子并不好求,因为我们并不知道式子中P(v? )的概率值。
不过,注意到既然不能求解P(v? ),那是否可以将这一项消去?
因此将求取P(y=1
v? )转化为求取P(y=1
v? )P(y=0
v? )。
P(y=1
v? )P(y=0
v? )=P(y=1)∏ni=1P(vj
y=1)P(y=0)∏ni=1P(vj
y=0)=∑i=1nlog(∏ni=1P(vj
y=1)∏ni=1P(vj
y=0))
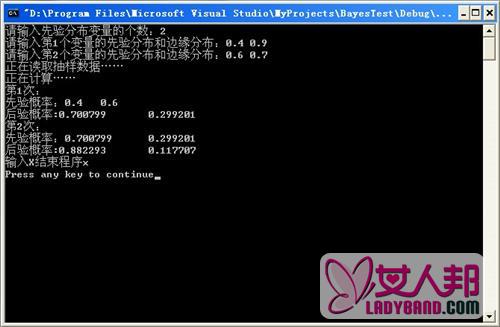
这里假定先验概率P(y=1)=P(y=0),y代表样本标签。
P(vi
y=1)~N(μ1i,σ1i)
P(vi
y=0)~N(μ0i,σ0i)
在分类阶段时,已经确定了第t帧中目标所在的位置,接下来来便更新学习机的参数。,会在目标框周围一定范围α内获取m个候选框(α代表到目标框中心位置的距离),将其定为正样本;然后在范围(α,β)内获取n个负样本框(m≈n)。得到正负样本后,便开始跟新分类器的参数,更新方式如下:
μ1i←λμ1i (1?λ)μ1
σ1i←λ(σ1i)2 (1?λ)(σ1)2 λ(1?λ)(μ1i?μ1)2??????????????????????????????????√
式子中的λ时学习参数。