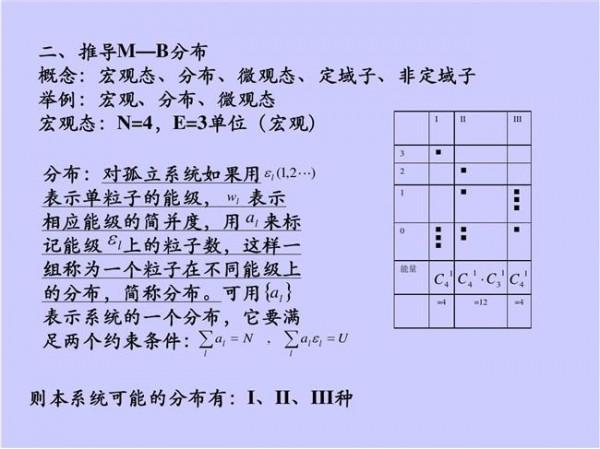
泰勒展开式是什么 cosx的泰勒展开为什么是求到奇次项

2017-12-26

字体:

大中小

浏览:

文章简介：给的导数阶数比较多(一般是证明题) 好多的极限也可以用泰勒公式(有比较典型的函数存在e^x,sinx,cosx .) 都不用余项余项.我一

给的导数阶数比较多(一般是证明题) 好多的极限也可以用泰勒公式(有比较典型的函数存在e^x,sinx,cosx .) 都不用余项余项.我一直都没有遇见过能用到余项的题很少用的这类型题太多了写几道不同类型的你看看 1 试确定ABC的值,使得 e^x(1 Bx Cxx)=1 Ax o(xxx) 其中o(xxx)表示x^3的三阶无穷小 2 设y=f(x)在(-1,1)内存在二阶连续导数且f''(x)不等于零求证 (1)对于(-1,1)内的任一x不等于0,存在唯一的t(x)属于(0,1),使得f(x)=f(0) xf'[t(x)x]成立 (2)lim t(x)=1/2 x--->0 3 泰勒公式求极限我觉得还是蛮不错的写两个最简单的就是那个意思吧 (1)lim 【e^x-1】/x=1 x-->0 众所周之这是个等价无穷小通过泰勒级数可以得到 e^x=1 x xx/2 xxx/3!

. 将这个e^x带入上面就可以得到1了 (2)lim sinx/x=1 x-->0 这也是个泰勒级数应用 sinx=x-xxx/3! x^5/5!-x^7/7! . 将sinx带进去得1 (3)lim [e^(-xx/2)-cosx]/x^4 x---->0 得1/12 你自己算算吧还得记住些重要函数的泰勒级数展开式 sinx cosx ln(1 x) arctanx e^x 很多都是通过这几个转变过来的 4 设f(x)在[0,1]上连续,(0,1)二阶可导,f''(x) 追问: 谢谢你,不过我不太懂你的意思,你可以告诉我cosx展开的证明过程吗?万分感激,谢谢…… gulumada280 2014-11-18