当年圆周率是怎么计算出来的?它的实质是什么?
圆周率的发展史 在历史上,有不少数学家都对圆周率作出过研究,当中著名的有阿基米德(Archimedes of Syracuse)、托勒密(Claudius Ptolemy)、张衡、祖冲之等。他们在自己的国家用各自的方法,辛辛苦苦地去计算圆周率的值。
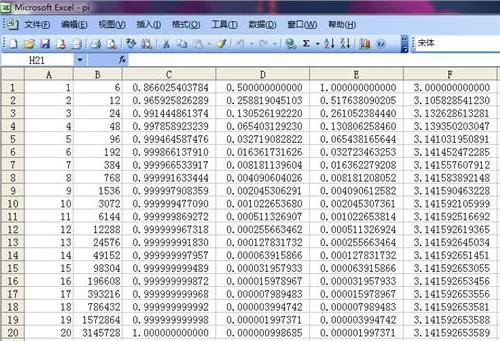
下面,就是世上各个地方对圆周率的研究成果。 亚洲 中国: 魏晋时,刘徽曾用使正多边形的边数逐渐增加去逼近圆周的方法(即「割圆术」),求得π的近似值3.1416。
汉朝时,张衡得出π的平方除以16等於5/8,即π等於10的开方(约为3.162)。虽然这个值不太准确,但它简单易理解,所以也在亚洲风行了一阵。 王蕃(229-267)发现了另一个圆周率值,这就是3.
156,但没有人知道他是如何求出来的。 公元5世纪,祖冲之和他的儿子以正24576边形,求出圆周率约为355/113,和真正的值相比,误差小於八亿分之一。这个纪录在一千年后才给打破。 印度: 约在公元530年,数学大师阿耶波多利用384边形的周长,算出圆周率约为√9.8684。 婆罗门笈多采用另一套方法,推论出圆周率等於10的平方根。 欧洲 ...
圆周率的发展史 在历史上,有不少数学家都对圆周率作出过研究,当中著名的有阿基米德(Archimedes of Syracuse)、托勒密(Claudius Ptolemy)、张衡、祖冲之等。他们在自己的国家用各自的方法,辛辛苦苦地去计算圆周率的值。
下面,就是世上各个地方对圆周率的研究成果。 亚洲 中国: 魏晋时,刘徽曾用使正多边形的边数逐渐增加去逼近圆周的方法(即「割圆术」),求得π的近似值3.1416。
汉朝时,张衡得出π的平方除以16等於5/8,即π等於10的开方(约为3.162)。虽然这个值不太准确,但它简单易理解,所以也在亚洲风行了一阵。 王蕃(229-267)发现了另一个圆周率值,这就是3.
156,但没有人知道他是如何求出来的。 公元5世纪,祖冲之和他的儿子以正24576边形,求出圆周率约为355/113,和真正的值相比,误差小於八亿分之一。这个纪录在一千年后才给打破。 印度: 约在公元530年,数学大师阿耶波多利用384边形的周长,算出圆周率约为√9.
8684。 婆罗门笈多采用另一套方法,推论出圆周率等於10的平方根。 欧洲 斐波那契算出圆周率约为3.1418。 韦达用阿基米德的方法,算出3.1415926535