狄拉克材料 狄拉克函数阅读材料

曹广福先生在新作《高等数学》中,开宗明义地讲:“数学教育过程是一个传授思想的过程”,而“微积分堪称古往今来数学史上最伟大的发明创造,其思想的光辉照耀着自然科学、社会科学的几乎每一个角落”。于是,曹先生提出一个问题:“如何运用数学的眼光去观察问题、思考问题”。

这里,曹先生引用了著名数学教育家Halmos的话:“具备一定的数学修养比具备一定的数学知识重要得多”。

如何才能有一定的数学修养,也是许多年轻学人关心的问题。 理工科学生都学过《高等数学》的相关内容。《高等数学》的讲授基本有两条思路,一是重视证明,一是重视计算。从而证明技巧与计算方法往往成了数学素修的表现形式。其实,数学的基本问题是发现,发现才是数学修养的核心。不知物理学人有没有如此感受。

简言之,发现就是于平常之中见异常。

在曹先生《高等数学》的第四页给出了一个赫维赛德函数

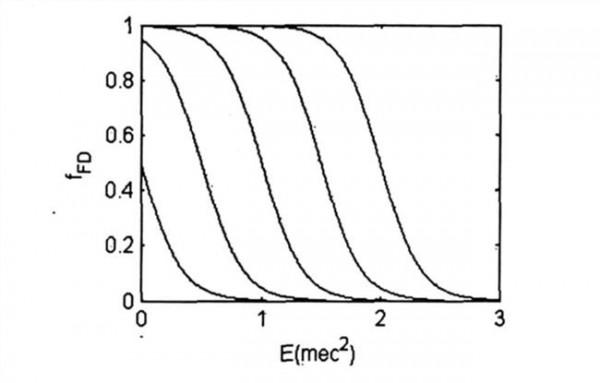
这是一个在零点不连续的函数,也是“函数都连续”的反例。其图象如下:

微积分研究的基本对象是连续函数,即乖孩子,赫维赛德函数不是一个“坏”孩子,只是有点调皮,比他“坏”的孩子有的是。赫维赛德函数调皮的地方是在任何一个非零点都可微,且导数为零,而在零点不可微,其右导数为零,左导数为无穷大。

反例往往产生新问题,也可能是新思想的产生点。数学物理学家狄拉克很喜欢这个调皮鬼。他把赫维赛德函数的“导函数”取名为δ函数,也就是后来人们常说的狄拉克函数,认为δ函数在非零点处的值为0,在零点处的值为无穷大,而且在整个实数轴上可积,其积分为1。这完全颠覆了数学家关于函数、可微、可积的概念。

狄拉克为δ函数找到一个用武之地,即分部积分:

显然,在右端的积分中完全与u(x)的导数无关。利用分部积分立即可得δ函数在实数轴上的积分为1。

如果认为维赛德函数H(t)的“导函数”为δ函数,那么当v(x)是连续函数时,用积分中值定理有大家熟悉的公式

这说明,δ函数作用的对象是一个函数,而不是一个实数,是一个将函数映射到实数集的映射,于是,人们把它叫做广义函数,有时又叫算子,这是一个有别于古典函数的一个新概念。这就是发现。现在知道,广义函数是局部凸空间上的连续线性泛函,已经属于现代泛函分析的范畴。

既然,δ算子作用的对象是一个函数,如果把函数看作是某个空间中的一个点,那么这个空间是多少维的呢?

这就要看这个空间的基底。如果这个函数可以展开成为傅立叶级数,即三角函数系是其基底,由于三角函数系是无穷多个,有整数那么多。于是,这个空间是无穷维空间,函数是无穷维空间中的一个点。因此,δ算子是无穷维空间上的算子,而经典微积分只是研究有穷维空间中经典函数的性质。有人把泛函分析叫做无穷维空间上的几何学

所以,δ函数是物理学中打开无穷维空间几何学的第一把钥匙。同时,可以看出,经典微积分通向无穷维空间的时空隧道有两个,一是分部积分,一是傅立叶级数。这就是经典微积分耀人的光辉。

δ函数通过分部积分通道,打开无穷维空间,把函数作为变量,在数理逻辑上,也使经典微积分从一阶逻辑走向高阶逻辑。

现在, 函数经常用于描述点源形成的场或一瞬时的量,例如点电荷、点热源、质点质量以及具有脉冲性质的物理现象等,并广泛应用于数学物理方程与场论,已成为大学本科的内容而没有什么新奇。其实,在物理上,连续分布的量与离散量并没有绝对的不同,只是在数学上才有根本的区别。这往往使数学家的思想没有物理学家那样的想象力。

爱因斯坦说:“想象力比知识更重要,因为知识是有限的,而想象力概括着世界上的一切,推动着进步,并且是知识进化的源泉。”

迪拉克是英国物理学家,中学时在职业学校读书,大概也不是什么重点中学。16岁上大学,本科学的是电气工程,21岁读数学方面的研究生,23岁开始研究由海森伯等人创立的量子力学,到24岁就发表题为《量子力学》的论文,并获剑桥大学物理学博士学位。1933年,与薛定谔、海森伯等共享当年诺贝尔物理学奖,时年31岁。

狄拉克是一个崇尚美感的数学物理学家,他执著地追求数学之美,如诗歌般工整美丽,他说:“我和薛定谔都极为欣赏数学美,这种对数学美的欣赏支配了我们的全部工作。”而海森堡在描述狄拉克创立量子力学的感受时,也说:“我窥测到一个异常美丽的内部,当想到现在必须探明自然界如此慷慨地展开在我面前的数学结构的这一宝藏时,我几乎晕眩了。

”我不知道狄拉克是不是诗人,但薜定谔就是一个很好的诗人,他把荷马史诗译成英文,还出版过诗集。