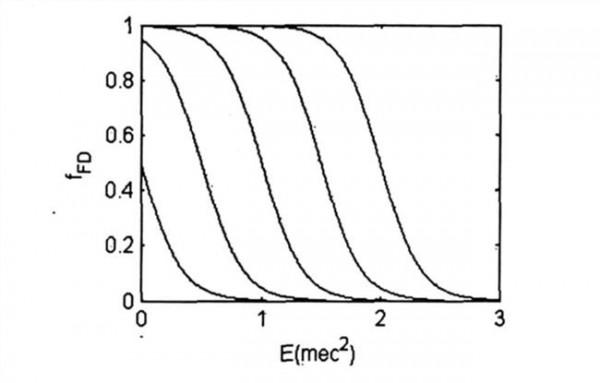
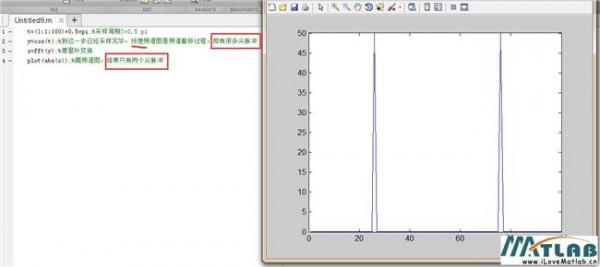
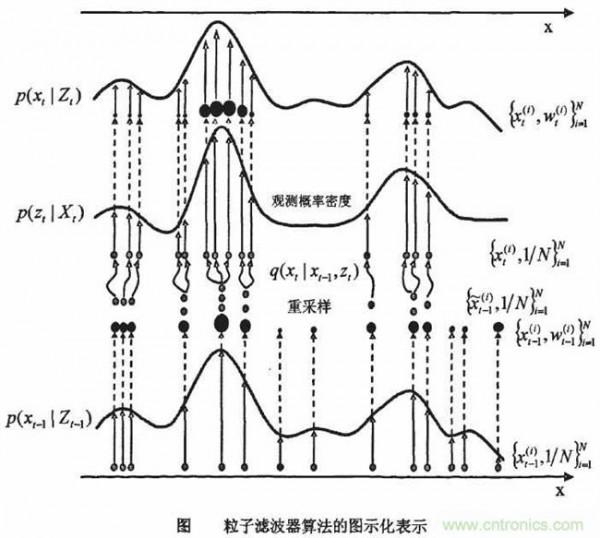
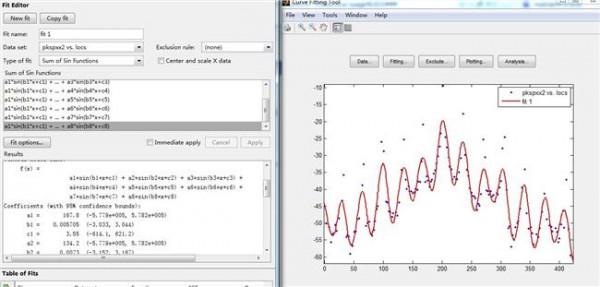
狄拉克分布 狄拉克函数的积分边界问题 下述等式成立吗?

购置税优惠即将到期,新一轮的汽车政策"山雨欲来".各类汽车政策当中,与汽车主机厂关联最大.消费者关注度最高的就是新能源车双积分(以下简称"双积分"),它甚至被看作是中国车市的一次战略性调整,因为一旦"双积分"全面落地实施,将大大影响乘用车的市场格局.亦步亦趋的意思是 "双积分"政策亦步亦趋新能源车将卖"白菜价"?什么是"双积分"?今年1~7月,新能源汽车产销分别完成27.2万辆和25.1

8月30日晚间,因2017年度不分红而站上舆论风口浪尖的格力电器,终于在披露2018中报业绩的同时公布了利润分配预案--公司拟以60.16亿

熊庆来是我国著名的数学家,推荐华罗庚"伯乐".其子熊秉明是欧华作协的早期会员.事实上,他不仅是一个作家,还是艺术家哲学家,是一位在西方传播中华文明的使者,深受学

主持人:各位搜狐的网友大家上午好,欢迎光临搜狐嘉宾聊天室.今天我们邀请的是文灯学校校长著名教育学家陈文灯老师,先请陈老师跟大家打个招呼.陈文灯:考研的朋友们,大家好.主持人:07年的研究生考试已经结束了,从07年的试卷来看,陈老师有一些简单的点评,对08年有一些什么新的启示吗?陈文灯:07年的试卷应该说难度并不大,但是它的知识面比较大,正是由于知识面比较大,同学们在这方面训练不够,所以07年同学们考试的成绩不如06年的成绩好. 我觉得今后可能关于解题的熟练程度还是要重点地抓,而且从试卷考核的情况

谢谢你的回答,对我启发很大;两端固定条件下确实比两端振动一致的约束要多,前者k取1到正无穷的 谢谢你的回答,对我启发很大;两端固定条件下确实比两端振动一致的约束

狄拉克简介英国理论物理学家保罗·狄拉克是20世纪伟大的物理学家,要对狄拉克进行评价,不就不得说他的贡献.狄拉克的照片诺贝尔物理奖对于物理学家可谓最好的褒奖,19

上册 第1章实数和数列极限 §1.1数轴 §1.2无尽小数 §1.3数列和收敛数列 §1.4收敛数列的性质 §1.5数列极限概念的推广 §1.6单调数列 §1.7自然对数底e §1.8基本列和收敛原理 §1.9上确界和下确界 §1.10有限覆盖定理 §1.11上极限和下极限 §1.12Stolz定理 §1.13数列极限的应用 第2章函数的连续性 §2.1集合的映射 §2.2集合的势 §2.3函数 §2.4函数的极限 §2.5极限过程的其他形式 §2.6无穷小与无穷大 §2.7连续函数 §2.8连

我觉得是成立的,我认为狄拉克函数可以理解为一阶无穷大,与一阶无穷小对应.假设一阶无穷小是dx,那么狄拉克函数可以理解为1/dx,题目中的狄拉克函数就是当x=a时,函数值为1/dx,别处的函数值都是0.既然定义了无穷大的阶,那么与无穷小的阶类似,任何常数乘以无穷大并不会改变阶数,只是原无穷大的一定的倍数,即原无穷大对某区间积分等于1,乘以某一个倍数积分就等于这个倍数了.很显然本题中的倍数应当是f(a).那么如何区分无穷大的阶数呢?个人认为可以通过积分来确定,如果经过在无穷区间上的积分后等于某一个常