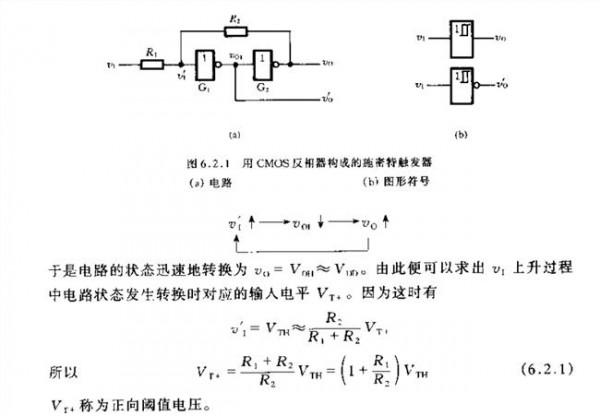
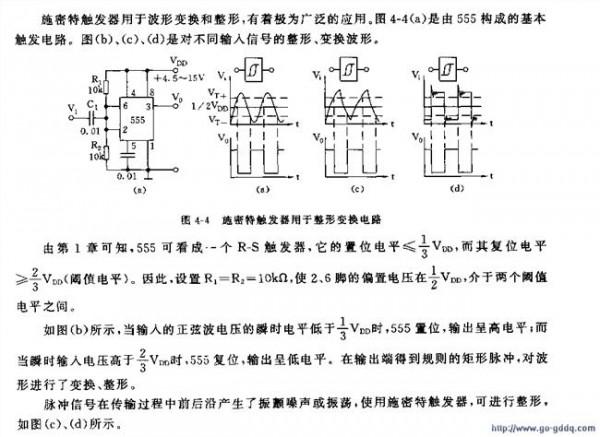
施密特正交化的几何意义是什么?
泻药。 方便说明我以欧式空间为例子来说明这个问题。 我们知道,对于一个平面上的两个向量,只需要以一个向量a1为基准,去除另一个向量a2在该向量上的投影,剩下的向量a2'就与a1正交。类似地,对于三维欧式空间,我们可以类似地去除掉a3与基准平面平行的向量,剩下的向量就与a1,a2张成的平面正交。
类似地,对于三维欧式空间,我们可以类似地去除掉a3与基准平面平行的向量,剩下的向量就与a1,a2张成的平面正交。
gram-schmit正交化的想法与上述过程完全类似。以一个向量为基准,得到第二个向量正交于第一个向量的部分;再得到第三个向量与第一、第二个向量都正交的部分;………如此不断做下去,就得到了一组正交的向量。
gram-schmit正交化的想法与上述过程完全类似。以一个向量为基准,得到第二个向量正交于第一个向量的部分;再得到第三个向量与第一、第二个向量都正交的部分;………如此不断做下去,就得到了一组正交的向量。