求助四维张量和三阶张量是不是指同一个东西?

2017-09-01

字体:

大中小

浏览:

文章简介：四维张量和三阶张量是不是指同一个东西.比如各向异性材料,杨氏模量为四阶张量;极化率为三阶张量;应力.应变为二阶张量.2楼: Original

四维张量和三阶张量是不是指同一个东西。比如各向异性材料,杨氏模量为四阶张量;极化率为三阶张量;应力、应变为二阶张量。

2楼: Originally posted by peterflyer at 2013-12-27 23:33:30四维张量和三阶张量是不是指同一个东西。比如各向异性材料,杨氏模量为四阶张量;极化率为三阶张量;应力、应变为二阶张量。

可不可以具体一点呢,比如说四维张量是几乘以几的矩阵。刚刚我还见到了“四维矢量(一阶张量)”和“四维二阶张量”这两个概念。这个怎么让人感觉几维几维和几阶几阶是一个平行的概念,我在电动力学中见到的二阶张量有九个分量,是不是说它们是三维二阶张量啊?

3楼: Originally posted by yixiao321 at 2013-12-28 00:01:53可不可以具体一点呢,比如说四维张量是几乘以几的矩阵。
刚刚我还见到了“四维矢量(一阶张量)”和“四维二阶张量”这两个概念。
这个怎么让人感觉几维几维和几阶几阶是一个平行的概念,我在电动力学中见到的二 ...

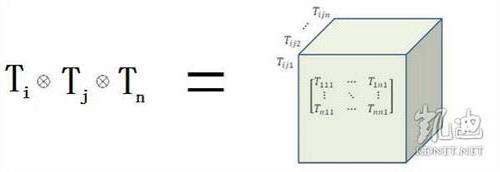
恕我孤陋寡闻,我还未听说几维什么张量的说法。四维张量有3^4=81个元素,三阶张量有3^3=27个元素,二阶有3^2=9个元素。

4楼: Originally posted by peterflyer at 2013-12-28 00:30:52恕我孤陋寡闻,我还未听说几维什么张量的说法。四维张量有3^4=81个元素,三阶张量有3^3=27个元素,二阶有3^2=9个元素。...

谢谢前辈,您说的这个关于张量的特点我很认同,一般书上也都是这样说明的。我现在正在看郭硕鸿先生编写的电动力学第三版,不知您现在手边有没有这本书,如果没有的话,网上已经有免费的电子版供下载了,书上第213页提到了四维张量这个概念,不过没有做说明,因此我很困惑,如果您方便的话是否可以查阅一下。

5楼: Originally posted by yixiao321 at 2013-12-28 00:46:23谢谢前辈,您说的这个关于张量的特点我很认同,一般书上也都是这样说明的。我现在正在看郭硕鸿先生编写的电动力学第三版,不知您现在手边有没有这本书,如果没有的话,网上已经有免费的电子版供下载了,书上第213页 ...

我下载了此书第三版,草草看了一下,在213页并未发现楼主所说的四维张量这个概念。我从未学过电动力学,对其知之甚少。不过根据楼主的叙述我推测,可能是指张量函数是四维函数---自变量x,y,z,t。比如应力σij(x,y,z,t)为四维二阶张量,其余依次类推。楼主认为呢?

6楼: Originally posted by peterflyer at 2013-12-28 01:09:53我下载了此书第三版,草草看了一下,在213页并未发现楼主所说的四维张量这个概念。我从未学过电动力学,对其知之甚少。不过根据楼主的叙述我推测,可能是指张量函数是四维函数---自变量x,y,z,t。比如应力σij(x,y ...

害前辈这么晚还没睡,实在对不住您先休息,等明天再回复吧。您是说张量矩阵元有这四个变量决定,不过二阶张量中的矩阵元个数仍为9个是吗?可是书中4.29矢(213页)T就是一个4×4的矩阵(式中a为4.27式),并且(4.29)式下面就说T即是四维张量。

“维”是指所在空间的维数;而“阶”则与坐标系转动下的变换性质有关。一般来说,m维空间中n阶张量的分量的个数有m的n次方个。“维”与“阶”不是一回事。

7楼: Originally posted by yixiao321 at 2013-12-28 01:48:20害前辈这么晚还没睡,实在对不住您先休息,等明天再回复吧。您是说张量矩阵元有这四个变量决定,不过二阶张量中的矩阵元个数仍为9个是吗?可是书中4.29矢(213页)T就是一个4×4的矩阵(式中a为4.27式),并且(4. ...

还以应力张量σij为例。它是二阶张量,一般情况下它有9个元素,在三维动力学问题中,它的每个元素都是x,y,z,t的四维函数,但由于对称性的原因,实际上只有6个元素,σij=σji;再比如材料的刚度系数,一般情况下是四阶张量,有81个元素,但由于能量守恒,实际上只有21个独立元素,若材料是各向同性的,就可进一步简化成2个:即各向同性材料的杨氏模量和波松比。