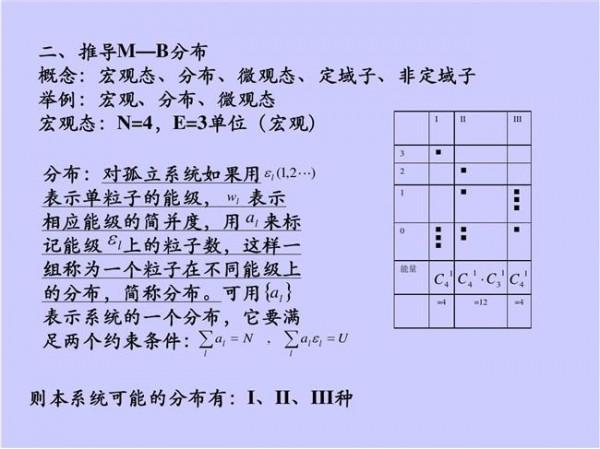
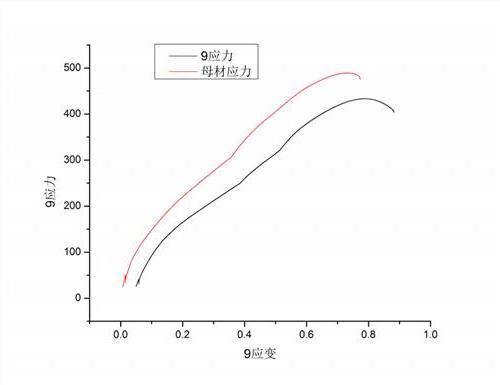
主应力和应力不变量推导
由上式可见,如果点的应力状态一定,则过该点任意斜面上的正应力和剪应力都将随着该斜面的法线方向余弦,也即l、m、n的数值而变化。
可以证明,必然存在着唯一的三个相互垂直的方向,与此三个方向相垂直的微分面上的剪应力恰为零,只存在着正应力。此正应力称为主应力,一般用表示。而相应的三个相互垂直的方向则称为主方向。与主方向一致的坐标轴叫做主轴。
下面讨论如何由已知的求主方向和主应力。假定法线方向余弦的斜切微分面正好是主平面,面上的剪应力为零,则由可得.于是,主应力在三个坐标轴上的投影分别为将式: 代入上列各式,经整理可得:
上式是以l、m、n为未知数的齐次线性方程组,其解就是主应力的方向,即应力主轴。此方程组一组解为,但由解析几何可知,方向余弦之间必须保持,它们不可能同时为零,因此不是方程组的解,该式存在非零解的条件是方程组系数所组成的行列式为零。展开行列式并考虑应力张量的对称性,则得:
可以证明,它必然存在三个实根,即主应力。
将求得的每一个主应力代入式中任意两个式子,并于联解,即可求得该主应力的方向余弦。这样,便可最终求得三个主方向。可以证明,这三个主方向是彼此正交的。
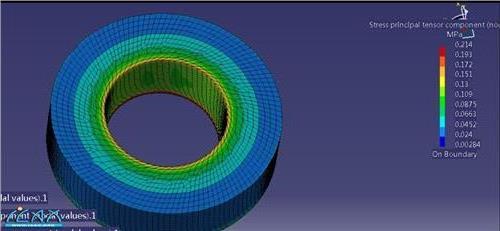

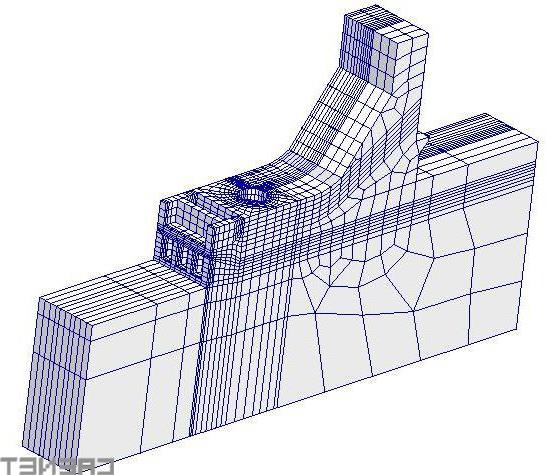

![崔京浩教授 崔京浩[清华大学教授]](https://pic.bilezu.com/upload/0/80/080d36167f0e8cef0bde2f7efa4d0cc5_thumb.jpg)