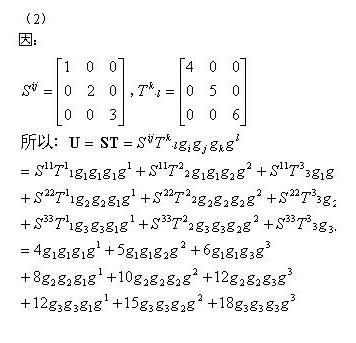
张量形式的缩并运算
y/jt之比是不定式,不失一般性可令其为1,张量分量Ui1 i2 i3… I k/j1 j2 j3… j s中出现了两个相 同的指标,按规定张量分量按这个指标从1到n求和。得到一个两阶数都降一阶的新张量。
若一个张量的两个坐标(张量的分量)满足Uij=Uji称此张量关于角标i,j对称。若一个张量的两个坐标(张量的分量)满足Uij=-Uji称此张量关于角标i,j反对称。两个张量形式相乘要注意张量分量的前后次序。
一个向量{x/1,x/2,……x/n}= x/1ɡ1+x/2ɡ2+……+x/nɡn的某个坐标x/i(1≤i≤n),对任何一个量c都有等式d(x/i+c)=dx/i成立,称向量在ɡi方向是平直的。如果向量在n个ɡi(1≤i≤n)方向都是平直的,称空间是平直的。
如果一个空间与它的共轭空间等式ɡ/i=ɡi(1≤i≤n)成立,此空间称为自共轭空间。既是自共轭空间又是平直空间就是欧几里得空间。若基底间的数积适合ɡi ɡj=δij,既当i=j时δij =1,当i≠j时δij =0。如果ɡi ɡj=0,称ɡi ,ɡj正交,(垂直的)。任何两个基底都正交的坐标系是笛卡儿直角坐标系,下面的讨论主要在这种坐标系中进行。
上述张量形式的定义都是在假定坐标系x/i,y/j是同一个顶点的情况下定义的,因而是与点有关的定义。也就是说假定张量的分量是n维空间某点的函数。当顶点在空间某区域M中变动时,每点处有一个张量形式,确定一个张量,于是得到一组张量形式,确定一组张量,称为M上的一个张量场。
张量形式的合并运算,张量形式的乘法运算,混合张量的缩并运算等运算对张量场也同样适用。若区域M中每一点处的微分空间里都有一个笛卡儿直角坐标系,M就是一个流形。
例如形式ds?=∑gijdx/idx/j满足条件∑gijdx/idx/j=∑gmndy/mdy/n省略和号得gijdx/idx/j=gmndy/mdy/n显然这是一个二阶协变张量形式,因此确定的张量是以gij或gmn为分量的二阶协变张量。
张量形式的乘法类似于多项式乘多项式。给出了张量乘张量结果,张量的☉积。n维空间上一个一阶张量就是向量,有n个坐标,既有n个张量分量。两个一阶张量相乘得二阶张量,有n?个张量分量(坐标)。一个r 阶张量乘一个t阶张量得一个r+t阶张量,共有n的r+t次幂个张量的分量。张量的乘法若是可交换的,这样得到的张量与其标号的次序无关。