索末菲边界条件 请教:周期性边界条件与波数的物理意义

谢谢你的回答,对我启发很大;两端固定条件下确实比两端振动一致的约束要多,前者k取1到正无穷的 谢谢你的回答,对我启发很大;两端固定条件下确实比两端振动一致的约束要多,前者k取1到正无穷的整数,后者k取负无穷到正无穷的整数。

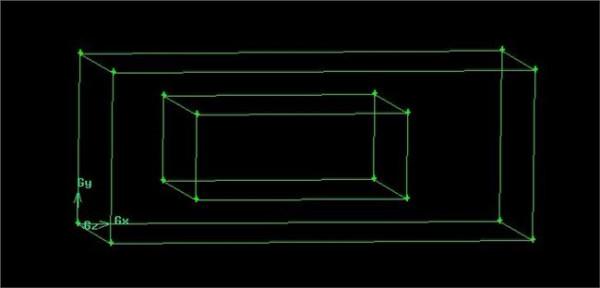
波尔的原子模型是不是也用到时了类似的原理?可不可以这么说:引入周期性边界条件是为了描述有限区域内自由电子的运动规律,并且不考虑表面效应,如果不引入的话电子的几率波会出现相消,即粒子会从有限区域内跑出去。是不是还可以推广一下:任意一个波长的波放在一个有限区域内都会自发形成驻波? ... Warrior Solo

波尔的原子模型可以认为是用的驻波的原理,至少一开始有这种思想,在初期,普朗克用波动方式对氢原子的电子处理的时候,就是把电子运动看成了驻波,那个圆周运动的周长就是波长的整数倍(也可能是半波长的整数倍吧记不太清楚了)。

其实E大说的对,用什么边界都行,那毕竟只是一种模型。周期性边界用数学处理的时候非常简便,因为有一个周期性边界的束缚。 非驻波不能长时间生存,但却不是完全不能生存,只是存在的时间很短,用一个式子来表达:δt*δv≈1(这个公式你可以自己推导下~)。

其中δt就是此波动的生存时间,其实也就是这一个波列的相干时间,另外相干长度δl=c*δt,其实就是波列的长度;而δv是此波的频率与对应的驻波频率之差的绝对值。

由此可见,如果有一堆相同原子处于激发态,如果原子的自发辐射对应的波列的长度越短,那么对应频谱展宽也就越大;如果相干长度很长,那么对应频谱就非常窄,比如说激光。如果波列无限长,那对应频谱就是一狄拉克函数了。

所以形成驻波也可以认为是一个自发的过程,因为在束缚条件下,非驻波的波通过刚才的公式消失了,留下了驻波。 我之前用腔中的电磁波类比,其实就是因为腔(金属腔)对电磁波的束缚跟周期性边界条件可以类比。 至于说电子,因为电子是用波函数来描述的(叫什么布洛赫波来着好像),所以,采用周期性边界条件这种模型的话,也是可以这样认为吧。