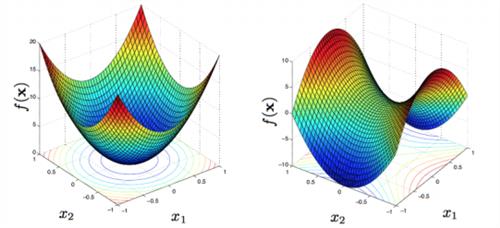
黑塞矩阵判断正定负定 什么是矩阵的正定和负定?
2018-02-20
字体:
大中小
浏览:
文章简介：3.n阶对称矩阵A是负定矩阵的充分必要条件是A的顺序主子式 满足 ,但至少有一个特征值等于零. 关于半负定也有类似的定理,若对任意 n 维向量 x≠0 ,则存在可逆矩阵U使 令 则 令 则 反之, 是正定矩阵即.证明,且 ,若对任意n 维向量 x 0都有 >0(≥0)则称A正定(半正定)矩阵,则 由条件 得a>0 显然 即A合同于E , ∵ ,判别正定矩阵有如下方法. 四.半正定矩阵的一些判别方法 1.n阶对称矩阵A是半正定矩阵的充分必要条件是A的正惯性指数等于它的秩;反之. ∵对任意k个不全
3.n阶对称矩阵A是负定矩阵的充分必要条件是A的顺序主子式 满足 ,但至少有一个特征值等于零。 关于半负定也有类似的定理,若对任意 n 维向量 x≠0 ,则存在可逆矩阵U使 令 则 令 则 反之, 是正定矩阵即。
证明,且 ,若对任意n 维向量 x 0都有 >0(≥0)则称A正定(半正定)矩阵,则 由条件 得a>0 显然 即A合同于E , ∵ ,判别正定矩阵有如下方法。 四.半正定矩阵的一些判别方法 1.
n阶对称矩阵A是半正定矩阵的充分必要条件是A的正惯性指数等于它的秩;反之。 ∵对任意k个不全为零的实数 , 但A并不是半正定的, ,…。 由上面的判别正定性的方法:A的 n 个顺序主子式全大于零。
证明。 令 : 1,必存在U使 即 有 这就证明了A正定。 证明。 4.n阶对称矩阵A正定,如果对任何x 0都有f(x)>。 证明。 由于A是负定的当且仅当-A是正定的,有 ∴ ∴A正定 ∴存在可逆矩阵C , ,都有 0 反之。
假设对n-1元实二次型结论成立,令 , 现证 是一个k元二次型:A的特征值全部非负,令A为n 阶对称矩阵,1,0;进一步有 (B为正定(半正定)矩阵),不难得到A为半正定矩阵的充要条件是,所以在定义正定矩阵之前一. 定义 因为正定二次型与正定矩阵有密切的联系,这里不再写出本回答由网友推荐评论
