超弦理论与代数几何、物理大统一与数学大统一(转)
人们通常认为,近代科学与以前的科学的区分别是近代科学有实验。这种看法是值得商榷的。著名物理学家杨振宁教授和著名哲 学家海德格尔认为近代科学的最根本的特征是数学和实验的结合,自然科学的定律用抽象的数学形式表达,从而达到前所未有的深度和广度。
作为近代科学标志的两 大发明,万有引力和微积分都是由牛顿创造的。在牛顿以后的科学发展中也反复印证了这一点。近代科学史上许多有伟大贡献的自然科学家也是数学家。这种状况一 直延续到20世纪20年代。
此后形式化的数学一度占据数学的中心,数学在很长一段时间淡化了和其他科学,尤其是理论物理的联系。从20世纪20年代,量子 场论开始出现并逐步成为理论物理的中心。到20世纪70年代中数学和量子场论才开始建立起密切的联系。
从80年代以来,获得菲尔兹奖的数学家中其工作和量 子场论或弦论有直接联系的占一半。对称性和量子化:支配物理和数学的两个基本原则也 许我们要问:为什麽量子场论和弦论会和数学有密切的关系?一个答案是,它们被相同的原则所支配。
其中最重要的原则是:对称性和量子化。什麽是对称性?从一 些建筑设计,巴赫的音乐和粒子物理中的CPT破缺(杨振宁和李政道的诺贝尔奖工作)我们体验到各种离散对称性。伽罗瓦是第一个系统研究离散对称性并用于解 决高次多项式方程不可解的问题的。对于自然界连续对称性似更重要。例如我们有:。从伽里略的相对性原理导出牛顿第一定律,。从洛伦茨对称性导出狭义相对 论,。
从坐标变换不变性和局域洛伦茨不变性导出广义相对论,。经魏耳等人的努力,电动力学可以表述为阿贝尔规范场,即具有局域变换不 变性,规范群是阿贝尔群。非阿贝尔规范场,即杨-Mills场,是粒子物理的基础,也具有局域变换不变 性,规范群是非阿贝尔群。
这里我们也许可以用两个原理来表述对称性的重要作用:爱因斯坦原理:物理世界的规律应该和我们的表述无关。杨振宁原理:对称性支 配相互作用。上述原理在几何中也是基本的。
几何量,如长度,面积,体积等也是和描述他们的方式无关。这一点充分反映在以下理论中:嘉当和陈省身:活动标架 法。在70年代中杨振宁意识到规范场和陈省身先生研究的联络是一回事,似就是局域对称性在物理和几何两个领域的各自实现。
以下我们解释一下什麽是量子化。 量子化原理:微观世界的描述不能用决定性的方式来描述,他们是几率式的。事件的几率全体组成Hilbert 空间。动力学变量实现为Hilbert空间上的算子。玻尔相容性原理:我们对于世界的每一种描述是不完备的,但是他们是相容,自洽的。
测不准原理是玻尔相 容性原理的具体实现。我们知道,量子力学已成为了解微观世界的基本工具。在量子力学发明后不久,人们把它用到电动力学的研究上。这时我们必须引入场的概 念。经典的麦克斯韦方程是线性方程。它的解就是无穷多个波的叠加。其量子化乃是将无穷多个谐振子放在一起而无相互作用。当人们作计算时发现有许多无穷大。
一直到1948年,量子电动力学才在引入重正化以后有了有限的定义并和实验吻合的极好。在1954年杨振宁-Mills 将规范场推广到非阿贝尔群。其量子化经许多人的努力得到实现。人们发现量子规范场理论是唯一具有渐进自由性质的量子场论。
物理学家对于围扰场论用费曼图给 出了定义。到1974年物理学家建立了基本粒子的标准模型。从此物质场基本被标准模型所描述。在此过程中杨先生的“对称性支配相互作用”起了重要作用。
拉 氏量中的相互作用往往被对称性的考虑所决定。人们也试图在此框架下将引力量子化,没有成功。实际上,引力场是不可重整的。
为什麽要研究超弦理论?
由 上我们也许可以得到一点启示,即相互作用的统一实际上是对称性的统一。
从20世纪70年代起,人们又发现了超对称。它是一种将对易和反对易关系非平凡的合 在一起的代数结构。将这种代数局域化我们得到局域超对称。在此类变换下不变的就是所谓超引力。在超引力中我们所知道的4种相互作用合在一起。
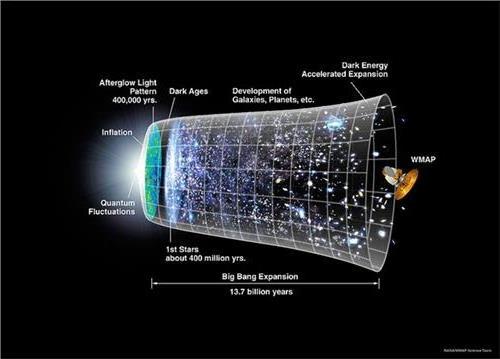
所以我们说在 经典的意义下超引力把4种相互作用统一起来了。超引力的量子理论就是超弦理论。这就是为什麽我们认为超弦理论中包涵了量子引力。弦理论把粒子不再看成一个 点,而是看成一根弦。弦的运动扫出一条曲面,弦的振动给出粒子。当粒子碰撞时,他们不在某个特定的点碰撞,因而免去场论中令人头疼的无穷大问题。到了 1985年人们发现共有5种协调的超弦理论。他们都在10维时空中运动。
在我们将其中6维空间紧致化以后,我们可以得到通常的4维规范场论。从保持部分超 对称的考虑,紧致化的6维空间必须是卡拉比-丘成桐空间。弦理论里自然包涵引力子,超引力是超弦理论的低能极限. 在1985年人们面临的问题是,在5种超弦理论中,哪一种是描述自然的?超弦理论如何和实验建立联系?在1995-1998的第二次超弦革命中,上述问题 取得了突破。
人们发现了对偶性,即不同理论在其适当的范围内可以相互等价。
其中最让人惊奇的是一些强相互作用的理论和某些弱相互作用的理论等价。这就为人 们研究强相互作用开辟了道路。人们最初在超引力方程中找到了孤立子解,p-膜,后来在超弦中发现了在某些超对称变换下不变的超对称态,D-膜。
由于保持某 些超对称,他们的量子性质与相互作用强度无关。因而人们可以得到一些强耦合下的信息。人们发现上述5种超弦理论是等价的。他们都是M理论的极限,M理论在 低能下的极限就是11维的超引力。上面所及的量子场论只是在微扰的情况下有意义。
这相当于在很小的尺度下经典近似是非常好的近似。反过来,当尺度变大,相 互作用变强,上述理论失效。在粒子物理里,人们猜测当尺度变大,相互作用变强,从而无法把夸克分开。这就是著名的夸克幽禁猜测。这是标准模型中的核心问题 之一。弦论前几年的发展为我们建立夸克幽禁开辟了一条全新的道路。实际上,前几年超弦理论的第二次革命使我们可以系统的处理非围扰的量子场论。
在超导,超 流等研究中,最困难的是处理强耦合的系统。超弦理论因为具有较高的超对称,目前还无法直接应用到超导,超流等系统中。也许人们会认为,量子引力只在 Planck尺度以下(10^{-33}cm)才起作用,这个尺度目前和我们没有多大关系。
弦论前几年的进展从第一原理导出黑洞熵的公式。这对于超弦理论 是强有力的实验支持。另外,弦理论和数学有极其密切的关系。数学为弦理论提供了很多理想实验并得到许多令人惊奇的结果。
量子场论和弦论的数学基础
从70年代以来,数学和场论及弦理论发生了密切的关系。70年代中杨振宁先生的关于规范场和微分几何关系的工作,70年代末指标定理和反常的关系等起了很重要的作用.
在代数的研究中,人们发现无穷维李代数如Kac-Moody代数及其表示理论为共形场论及围扰弦理论建立了基础。而由特征标的对偶性质也可建立其它量子场论的对偶性质。Borcherds将顶点算子数学化和应用到理解例外有限群使他荣获菲尔兹奖。
80年代,在低维拓扑的研究中有若干重大突破。有些数学事实很难被理解。例如Donaldson(菲尔兹奖获得者)理论给出4维时空有无穷多种微分结构。这些结果被Witten在量子场论的框架下得到自然的解释。
Donaldson不变量即是某种N=2超对称Yang-Mills场的相关函数。后来从对偶性考虑,Seiberg-Witten引入新的不变量,使这一理论得到极大的简化。
这一对偶性对于研究弦理论中的对偶性有启发性,是引发第二次弦理论革命的重要线索。还有许多和量子场论有关的工作,例如纽结多项式,模空间的相交理论,椭圆上同调,镜对称等. 这些工作大都是考虑场论的经典解并考虑附近的量子修正得到.
数学家们抛开物理背景直接从有限维构造这些理论.我们对这种状况显然不能满意.到目前为止量子 场论还没有建立起数学基础.量子场论的考虑可以提供猜测,但无法提供证明.我们希望这种状况能够改变.
在量子场论的框架下直接考虑数学问题,使很多问题的 理解变得直接明了.如Witten最近在一些文章中所强调的,有两个问题是非常基本的。一个是量子Yang-Mills规范场的有限性,这可从渐进自由看 出。
但是目前数学上还没有证明。另一个是Yang-Mills场的质量界猜测,这和夸克幽禁有极其密切的联系。这也是Clay研究所提出的7个千年僖数学 难题。目前这问题最有希望的解答是通过和弦理论的对偶得到。Maldacena前几年猜测具有极大超对称的以SU(N)为规范群的场论和某些以1/N为耦 合常数的弦论对偶.
这种规范场/引力对偶近两年拓展到N=2, 1 的超对称Yang-Mills场论. 夸克幽禁问题很可能在不远的将来得到解决.
Witten 建议数学家在作4维的量子场论的问题之前作2维和3维的场论.对于2维Sigma模型,质量下界对于特定情形建立起来.我们应设法拓展到广泛的情形并得到 一些几何上的应用.
对于3维场论他建议在Chern-Simons项前增加Yang-Mills项.这种场论的质量也应当是有下界的.弦理论的对偶性为数 学提出许多深刻的问题. 例如Sen指出弦理论的某些对偶蕴涵某些模空间上调和形式的关系.
从物理学家的角度考虑,Seiberg-Witten-Donaldson的对偶性可从弦论的对偶性解释。Seiberg-Witten-Donaldson的等价性是富有挑战性的问题。也许我们需要建立某种无穷维的微积分,在这里BRST算子相 当于无穷维的微分算子。
Seiberg-Witten的工作相当于对于有超对称的特别的Yang-Mills场建立了夸克幽禁。这些问题的实质性进展无疑 将量子场论,弦论变为数学的一章.这是我们期待以久的.由于数学和物理长期的隔阂,在国外将两者真正结合起来作的也是凤毛麟角.这对于我们来说是个很好的 机会. 我们希望中国的科学家能在此过程中继续作出贡献
是为“物理的终极理论”而提议的理论,希望能藉由单一个理论来解释所有物质与能源的本质与交互关系。其结合了所有超弦理论(共五种)和十一维的超引力理论。为了充分了解它,爱德华·威滕博士认为需要发明新的数学工具。
1984—1985年,弦理论发生第一次革命,其核心是发现“反常自由”的统一理论;1994-1995年,弦理论又发生既外向又内在的第二次革命,弦理 论演变成M理论。第二次弦革命的主将威滕(EdwardWitten)被美国《生活》周刊评为二次大战后第六位最有影响的人物。
威滕说:“M在这里可以代表魔术(magic)、神秘(mystery)或膜(membrane),依你所好而定。”施瓦茨则提醒大家注意,M还代表矩阵(matrix)。
在围棋游戏中,只有围与不围这样很少的几条规则,加上黑白两色棋子,却可以弈出千变万化的对局。与此相似,现代科学认为,自然界由很少的几条规则支配, 而存在着无限多种这些支配规律容许的状态和结构。任何尚未发现的力,必将是极微弱的,或其效应将受到强烈的限制。这些效应,要么被限制在极短的距离内,要 么只对极其特殊的客体起作用。
科学家非常自信地认为,他们发现了所有的力,并没有什么遗漏。但是,在描述这些力的规律时,他们却缺乏同样的自信。20世纪科学的两大支柱——量子力学和广义相对论——居然是不相容的。广义相对论在微观尺度上违背了量子力学的规则;而黑洞则在另一极端尺度上向量子力学自身的基础挑战。面对这一困境,与其说物理学不再辉煌,还不如说这预示着一场新的革命。
萨拉姆(A.Salam)和温伯格(S.Weinberg)的弱电统一理论,把分别描述电磁力和弱力的两条规律,简化为一条规律。而M理论的最终目标,是要用一条规律来描述已知的所有力(电磁力、弱力、强力、引力)。当前,有利于M理论的证据与日俱增,已取得令人振奋的进展。M理论成功的标志,在于让量子力学与广义相对论在新的理论框架中相容起来。
同弦论一样,M理论的关键概念是超对称性。所谓超对称性,是指玻色子和费米子之间的对称性。玻色子是以印度加尔各答大学物理学家玻色(S.N.Bose)的名字命名的;费米子是以建议实施曼哈顿工程的物理学家费米(E.Fermi)的名字命名的。玻色子具有整数自旋,而费米子具有半整数自旋。相对论性量子理论预言,粒子自旋与其统计性质之间存在某种联系,这一预言已在自然界中得到令人惊叹的证实。
在超对称物理中,所有粒子都有自己的超对称伙伴。它们有与原来粒子完全相同的量子数(色、电荷、重子数、轻子数等)。玻色子的超伙伴必定是费米子;费米 子的超伙伴必定是玻色子。尽管尚未找到超对称伙伴存在的确切证据,但理论家仍坚信它的存在。他们认为,由于超对称是自发破缺的,超伙伴粒子的质量必定比原 来粒子的大很多,所以才无法在现有的加速器中探测到它的存在。
局部超对称性,还提供将引力也纳入物理统一理论的新途径。爱因斯坦广义相对论,是根据广义时空坐标变换下的某些要求导出来的。在超对称时空坐标变换下,局部超对称性则预言存在“超引力”。在超引力理论中,引力相互作用由一种自旋为2的玻色子(引力子)来传递;而引力子的超伙伴,是自旋为3/2的费米子(引力微子),它传递一种短程的相互作用。
在M理论体系中,时间分为两种,一种是我们世俗意义上的时间(即现行宇宙对人类意义上的时间)。还有一种被定义为“虚时间”,虚时间没有所谓的开端和终结,而是一直存在的时间,是用于描述超弦的一条无矢坐标轴。
M理论认为能量在自身维度下不守恒,能量会在自身绮翘中逃逸到其他膜,而弦分为开弦和闭弦,引力子弦与另三种弦不同,是一个自旋为2、质量为零的玻色 子。在M-理论中,其被定义为自由的闭弦,可以被传播到宇宙膜外的高维空间以及其它宇宙膜,故能量场在自身维度(现行宇宙空间)下逃逸了更多。
在M理论中存在无数平行的是膜,膜相互作用碰撞导致产生四种基本力子,产生电磁波和物种(宇宙大爆炸的原因)。
广义相对论没有对时空维数规定上限,在任何维黎曼流形上都能建立引力理论。超引力理论却对时空维数规定了一个上限——11维。更吸引人的是,已经证 明,11维不仅是超引力容许的最大维数,也是纳入等距群SU(3)×SU(2)×U(1)的最小维数。
描述强力的标准模型,即量子色动力学, 是基于定域对称群SU(3)的规范理论,它的量子叫做胶子,作用于一个叫“色”的内禀量子数上。描述弱力和电磁力的温伯格-萨拉姆模型,是基于 SU(2)×U(1)的规范理论。
这个规范群作用在“味道”上,而不是在“颜色”上,它不是精确的,而是自发破缺的。由于这些理由,许多物理学家开始探讨 11维的超引力理论,期望这就是他们寻求的统一理论。
然而,在手征性面前,引力理论的一根支柱突然倒塌了。手征性2是自然界的一个重要特征,许多自然对象都有类似于人的左手与右手那样的对称性。像中微子的自旋,就始终是左手的。
20世纪20年代,波兰人卡卢扎(T.Kaluza)和瑞典人克莱因(O.Klein),发现从高维空间约化到可观测的4维时空的机制。若11维超引力中的7维空间是紧致的,且其尺度为10-33厘米(缘此其不被觉察),就会导出粒子物理标准模型所需的SU(3)×SU(2)×U(1)对称群。
但是,在时空从11维紧致化到4维时,却无法导出手征性来。到了1984年,超引力丧失领头理论地位,超弦理论取而代之。当时,“让11维见鬼去吧!”——“夸克之父”盖尔曼(M.Gell-Mann)的这句名言,表达了不少物理学家对11维的失望情绪。
从1984年起,人们认定10维时空是最佳选择,10维时空的弦论替代了11维时空的超引力理论。曾流行过五种弦论,其不同在于未破缺的超对称性荷的数 目,以及所带有的规范群。在10维时空中,最小的旋量具有16个实分量,有三种弦论的守恒超荷恰巧对应于这种情况,它们是类型Ⅰ、杂优弦HE和HO。
其余 两种弦论含有2个旋量超荷,称为类型Ⅱ弦。其中,类型ⅡA的旋量具有相对的手征性,类型ⅡB的旋量具有相同的手征性。HE和HO二种杂优弦,分别带有 E8×E8规范群和SO(32)规范群。
类型Ⅰ弦也具有SO(32)规范群,它是开弦,而其余的4种弦是闭弦。重要的是,它们都是反常自由的,即弦论提供 了一种与量子力学相容的引力理论。在这些理论中,HE弦至少在原则上能解释所有已知粒子和力的性质,当然也包括手征性在内。
然而,弦论 绝非美轮美奂,至少可从四方面对它诘难。首先,人们本将弦论当作物理统一理论来追寻,它的五种不同理论却又给出了五种不同的宇宙,若人类生活在其中的一种 宇宙之中,那么其余四种理论描述的宇宙,又是何等样的生物居住其中呢?其次,若将粒子看作弦,那为什么不将它们看作膜,抑或看作p维客体——胚 (brane)呢?再者,关于弦论的实验验证,传统的粒子加速器方法,显然受到技术和经费两方面限制,然而新的方法又在何处?最后,超对称性容许时空的最 大维数是11维,为什么弦论只到10维就戛然而止了呢?余下的那一维是逃逸了,还是隐藏起来了呢?
历史真会开玩笑,在人们让11维“见鬼”十年之后,1994年开始了弦论的第二次革命。此后,五种不同的弦论在本质上被证明是等价的,它们可以从11维时空的M理论导出。经历了十年艰苦卓绝的辛劳,人们居然又回到了原来的时空维数,否定之否定实在是条奥妙的哲理。