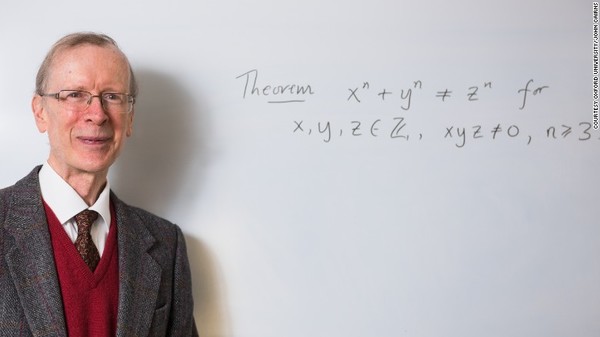怀尔斯在牛津 安德鲁·怀尔斯 牛津大学教授

安德鲁·怀尔斯是当代著名的英国数学家,因证明了著名的费马猜想名闻天下。费马猜想最初出现在费马的《页边笔记》中。尽管费马表明他已找到一个绝妙的证法而由于页边空位不足没有写出。但这个“恼人”的费马猜想却需要数学家们经过三个多世纪的努力来证明,最终使得费马猜想变成了“费马大定理”。

首先让我们来认识下这个困扰数学家350多年的费马猜想是什么。其实,问题非常简单,它是用一个每个中学生都熟悉的数学定理——毕达哥拉斯定理来表达的。毕达哥拉斯定理说:在一个直角三角形中,斜边的平方等于两直角边的平方之和。

即X2 Y2=Z2。大约在公元1637年前后 ,当费马在研究毕达哥拉斯方程时,他写下一个方程,非常类似于毕达哥拉斯方程:X^n Y^n=Z^n,当n大于2时,这个方程没有任何正整数解——这就是费马猜想。下面我们再来认识一下揭开这个奥秘的人。

1953年,怀尔斯出生在英国剑桥,少年时代的怀尔斯便近乎疯狂似的迷上数学了。一天,小怀尔斯在街上的图书馆看见了一本书,这本书只有一个问题且没有答案,怀尔斯被吸引住了。这就是E?T?贝尔写的《大问题》。它叙述了这个让一个又一个的数学家望而生畏并且几百年来无人能解的费马猜想。

安德鲁·怀尔斯被费马猜想吸引住了,他决定解决这个问题,从此选择了数学作为终身职业。研究生毕业后,为了能够完成费马猜想的证明,怀尔斯作了一个重大的决定:要完全独立和保密地进行研究。怀尔斯放弃了所有与证明费马猜想无直接关系的工作,几乎所有的时间都投入到这个问题中来。在家里的顶楼书房里他开始了证明费马猜想的战斗。

谁也没有想到,这场战斗,一打就是七年。

经过7年不知日夜的努力,怀尔斯终于完成了费马猜想的证明。1993年6月23日,怀尔斯在英国牛顿研究所举行了20世纪最重要的一次数学讲座。两百名数学家聆听了这一演讲,但他们之中只有四分之一的人完全懂得黑板上的希腊字母和代数式所表达的意思。

其余的人来这里是为了见证他们所期待的一个真正具有意义的时刻。他的长达200页的论文大量地依赖于环论和群论地结果。由于他的良好声誉,更由于他的论文是建立在对此问题有深入刻画的结果基础上,同行专家相信怀尔斯已经打开了许多人无法打开的成功之门。怀尔斯的事迹随之通过报刊杂志被新闻界广为宣传,《纽约时报》甚至还将他的故事搬到了报纸的头版。

然而当怀尔斯成为媒体报道的中心时,证明的一个缺陷被发现了。

1993年8月23日,审稿人尼克?凯兹发现了证明中的一个小缺陷。数学的绝对主义要求怀尔斯无可怀疑地证明他的方法中的每一步都行得通。怀尔斯以为这是一个小问题,补救的办法可能十分容易就能找到便没有注重这个问题。

可是6个多月过去了,这个错误还是没有能够得到解决,怀尔斯正处在崩溃的边缘,他准备承认失败。经过长时间的考虑后,怀尔斯决定邀请剑桥大学的讲师理查德?泰勒到普林斯顿和他一起工作,希望两人一起能够找到解决这个问题的方法。可是到了9月,依然没有结果,万般无奈之下,他们二人不得不准备放弃了。令人惊讶的是,9月19日在怀尔斯对论文做最后一次检验的时候,问题的答案终于浮出了水面。

八年的岁月,穷其一身之技,怀尔斯终于向世界证明了他的才能。世界不再怀疑这一次的证明了。这两篇论文总共有130页,是历史上核查得最彻底的数学稿件,它们发表在1995年5月的《数学年刊》上。数学家约翰?科茨说:“用数学的术语来说,这个最终的证明可与分裂原子或发现DNA的结构相比,对费马猜想的证明是人类智力活动的一曲凯歌,同时,不能忽视的事实是它一下子就使数学发生了革命性的变化。

对我说来,安德鲁成果的美和魅力在于它是走向代数数论的巨大的一步。”

这一次,怀尔斯终将凭借自己的智慧和对数学事业的百分之百的认真严谨而载入史册。