泰勒展开式应用 泰勒公式及其应用典型例题
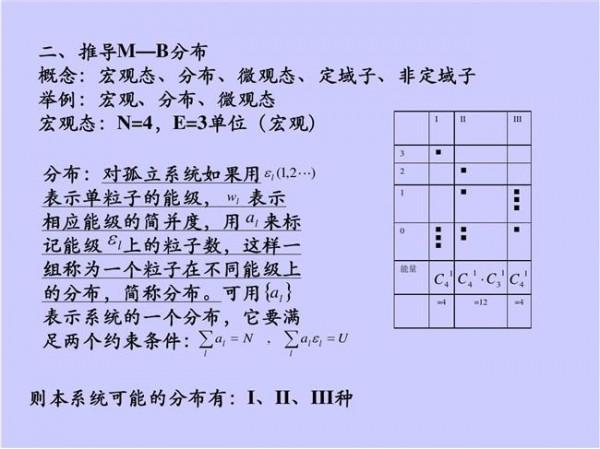
泰勒公式及其应用典型例题 泰勒公式及其应用 常用近似公式 ,将复杂函数用简单 的一次多项式函数近似地表示,这是一个进步。当然这种近似表示式还 较粗糙(尤其当 较大时),从下图可看出。 上述近似表达式至少可在下述两个方面进行改进: 1、提高近似程度,其可能的途径是提高多项式的次数。
2、任何一种近似,应告诉它的误差,否则,使用者“ 心中不安”。 将上述两个想法作进一步地数学化: 对复杂函数 希望 ,想找多项式 来近似表示它。
自然地,我们 所具有的性态 —— 如:在某点 的形式如何确定; 。 近似 所 尽可能多地反映出函数 处的值与导数值; 我们还关心 产生的误差 【问题一】 设 于 在含 的 的开区间内具有直到 次多项式 阶的导数, 能否找出一个关 近似 ? 【问题二】 若问题一的解存在,其误差 的表达式是什么? 一、【求解问题一】 问题一的求解就是确定多项式的系数 。
????? 上述工整且有规律的求系数过程,不难归纳出: 于是, 所求的多项式为: (2) 二、【解决问题二】 泰勒(Tayler)中值定理 若函数 则当 在含有 时, 的某个开区间 可以表示成 内具有直到 阶导数, 这里 是 与 之间的某个值。
先用倒推分析法探索证明泰勒中值定理的思路: 这表明: 只要对函数 反复使用 【证明】 以 函数 且 与 为端点的区间 或 记为 , 。 阶的导数, 及 在 与 之间 次柯西中值定理就有可能完成该定理的证明工作。
在 上具有直至 函数 且 在 上有直至 阶的非零导数, 于是,对函数 有 及 在 上反复使用 次柯西中值定理, 三、几个概念 1、 此式称为函数 或者称之为函数 当 按 在点 的幂次展开到 处的 阶的泰勒公式; 阶泰勒展开式。
时, 泰勒公式变为 这正是拉格朗日中值定理的形式。 因此,我们也称泰勒公式中的余项。 为拉格朗日余项。 2、对固定的 ,若 有 此式可用作误差界的估计。
故 表明: 误差 是当 时较 高阶无穷小, 这一余项 表达式称之为皮亚诺余项。 3、若 ,则 在 与 之间,它表示成形式 , 泰勒公式有较简单的形式 —— 麦克劳林公式 近似公式 误差估计式 【例 1】求 解: 的麦克劳林公式。
, 于是 有近似公式 其误差的界为 我们有函数 (1)、 的一些近似表达式。 (2)、 (3)、 在 matlab 中再分别作出这些图象,观察到它们确实在逐渐逼近指数函 数。
【例 2】求 的 阶麦克劳林公式。 解: 它们的值依次取四个数值 。 其中: 同样,我们也可给出曲线 出它们的图象。 的近似曲线如下,并用 matlab 作 【例 3】求 的麦克劳林展开式的前四项,并给出皮亚诺余项。
解: 于是: 利用泰勒展开式求函数的极限,可以说是求极限方法中的“终极武 器”, 使用这一方法可求许多其它方法难以处理的极限。 【例 4】利用泰勒展开式再求极限 解: , 。 【注解】 现在,我们可以彻底地说清楚下述解法的错误之处 因为 ,从而 当 时, ,应为 的近似值, 并估计误差。 【例 5】利用三阶泰勒公式求 解: 故: