刘徽九章算术割圆术 为《九章算术》作注的数学泰斗刘徽

刘徽,邹平县人,魏晋时期的数学家,主要生活在三国时代,著有《九章算术注》等,是中国古代杰出的数学家。

刘徽于魏景元四年(263年)完成了为《九章算术》作注的工作。《九章算术》是现存最早的中国古典数学名著,它系统总结了先秦至两汉时期中国数学的重大成就,是中国古代数学体系形成的显著标志。全书分为9章,采用问题集形式,收集了246个数学问题和有关解题方法,但对其中用到的公式、定理却没有给出证明,使人难以了解其各种算法的数学原理及其内在的逻辑联系。

刘徽的《九章算术注》是具有高度创造性的科学论文。他一面阐述每个具体算法的理论依据,一面揭示各种算法之间的内在联系,对数学概念分别给以定义;对公式、定理一一加以证明;解题过程详加分析,并提出了很多独创的见解,体现了严谨的逻辑思维和深刻的数学思想,为中国古代数学奠定了坚实的理论基础。

《九章算术》本来有九章,刘徽加上了自己的一章,即第十章,叫《重差》,里边都是关于海岛的高、宽计算的题,因此,印行单行本时叫做《海岛算经》。《海岛算经》是一部测算专著,它所揭示的重差测量理论和方法,成为古代测量的基本依据,为实现由直接测量向间接测量的飞跃架起了桥梁。

刘徽生平事迹不为人知,生卒年月无考。在中国古代,像刘徽这样职业进行科学研究的人,必须具备两个条件,第一是爱好,第二是家庭富裕。为了研究和印刷书籍,他个人要投入大量的精力和资金,没有坚强的经济基础是万万不能的。

关于他的情况,仅存的史料是他为《九章算术注》的序:“徽幼习九章,长再详览。观阴阳之割裂,总算术之根源,探赜之暇,遂悟其意。是以敢竭顽鲁,采其所见,为之作注。”宋徽宗大观三年(1109年),追封古代数学家爵位,封其为“淄乡男”。

刘徽一生集前人大成,在数学上有许多杰出的创造。他精辟地研究了开方不尽数,用首创的十进分数(小数的前身)来刻画它们,向着无理数的认识迈出了重要的一步。为证明圆面积公式,他创造了割圆术,从圆内接正六边形开始,以边数逐次倍增的圆内接正多边形的面积去逼近圆面积,并算出一圆内接正3072边形的面积,得到圆周率的近似值为3.

1416。为了求得由底为直角三角形的直棱柱分割而成的一个四棱锥与一个三棱锥的体积之比,他采用无限分割、逐次拼合的方法建立了“刘徽原理”。

在研究各种体积问题时,他又创造性地运用两立体图形相应截面面积之间的关系确定它们体积之间的关系,被称为“刘祖原理”。刘徽提出并定义了许多数学概念,如幂(面积)、方程(即线性方程组)、正负数等。他对《九章算术》中的分数理论、比率理论、方程理论、勾股理论也都做出了重要贡献。

第一,极限思想。刘徽为证明《九章算术》中的各种公式,提出了“析理以辞,解体用图”的要求,并创立了对许多问题行之有效的图验法和棋验法。但是有些问题并非仅仅用棋用图就可以解决的,而是需要具备相当清楚的极限思想。

刘徽则把极限思想和极限概念运用于解决实际的数学问题,这是极为重要的。刘徽创立割圆术,用圆内接正多边形面积逼近圆面积,用圆内接正多边形周长逼近圆周长,解决了推求圆周率精确值问题,是他应用极限思想的成功事例。

他处理弧田术(弓形面积公式)的作法,开方不尽时求微数的思想,以及对两立体截面积与体积关系的认识,无不与极限和无穷小分割的思想紧密地联系在一起。这些思想具有深刻的数学内涵,并且是解析几何、微积分等现代数学方法的基础。

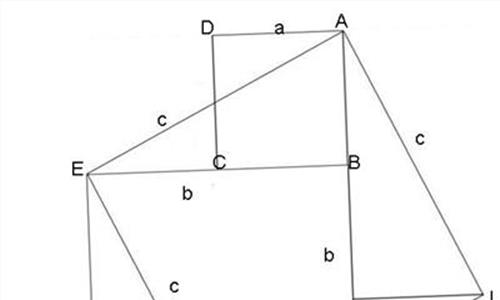
第二,勾股定理和重差术。勾股定理是中国古代几何学中一个最基本的定理。刘徽在《九章算术注》中明确地提出“出入相补,各从其类”的出入相补原理。这个原理的内容是几何图形经分合移补所拼凑成的新图形,其面积(或体积)不变。

刘徽根据出入相补原理证明了勾股定理,改进了勾股数的计算公式,并将其广泛应用于解决勾股容方、勾股容圆和立体体积等各种几何问题。勾股测量是勾股定理的一项重要实际应用。东汉时期的天文学家和数学家创立重差术用于测算太阳的高度和距离。

刘徽在《海岛算经》中通过实例,对于重差术作了系统的总结,并且提出根据三次和四次测量结果的推算公式,用以解决复杂的测量问题。重差术是当时世界上最先进的用于测量的数学方法。

第三,割圆术和圆周率。两汉之前,我国一般采用的圆周率是“周三径一”,即π=3。但是,这个数值误差很大。刘徽的主要贡献之一是在《九章算术注》中首创了“割圆术”,用圆内接正多边形的周长和面积逼近圆周长和圆面积,为圆周率研究工作奠定了理论基础和提供了科学的算法。

正如他所指出的“割之弥细,所失弥少。割之又割,以至于不可割,则与圆合体而无所失矣”,即极限情形是两者完全重合。刘徽求出π值为3.1416,约值为3.14,后人为纪念刘徽的贡献,将3.14称为徽率。刘徽之后,祖冲之把圆周率推算到更加精确的小数点后七位,这是当时世界上最先进的成果。