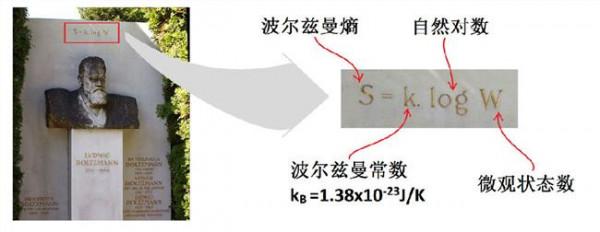
玻尔兹曼熵公式 【求助】关于玻尔兹曼公式
是一种构型还是一种状态?楼主是说“能量低的构型,在数量上会占有优势”,这个话是有点缺陷的。 比如A-B合金(固溶体),我现在有一个1000原子的体系,其中998个A,2个B。考虑三个构型: 甲:2个B原子是最近邻。
乙:2个B原子距离很远(比如20个晶格),可以忽略2个B之间的相互作用 丙:2个B原子距离也很远,但两个B原子的位置和构像乙不同。 假定甲的能量较高,而乙和丙的能量应该是一样的。 按照楼主所说的玻尔兹曼分布,乙和丙的能量低于甲,它们出现的概率应该是大于甲的,但是我们具体到一个构像来说,你怎么样证明一个体系中乙构像的数量很多,或者丙的数量很多?你用MC方法,可以得到很多的乙构像么?实际上,与乙和丙构像的能量相等的构像有很多,我们只能说这样的能量状态的构像是很多的,而不是说乙构像很多,或者丙构像很多。
再换一个情形,假如构像甲的能量较低呢?你用任何方法,会不会得到很多的甲构像?三楼yahoohoo 说得很清楚,最可几的状态,并不是能量最低的状态。
楼主的说法,我感觉混淆了一些概念,主要是把一个确定的原子排布(即所谓的构型、构像,它代表的只是一个微观状态,是排列组合中的一员),与一个能量状态理解成同一回事,二是把状态变化的能量判据与热力学微观状态数相联系,并把能量最低当成了热力学几率最高,三是可能搞混了统计力学中概率密度与概率的概念。
一个给定的宏观状态下的体系,它的微观状态(即可能的构像分布)是很大量的,其中能量低的构像,它对系统总能量的贡献较大,这是MC方法中Metropolis重要性取样的基本原理。
但要注意,是分布的概率密度与玻耳兹曼因子成正比,而不是它出现的概率本身与玻耳兹曼成正比。
总体上,我的理解和Yahoohoo的理解是相近的。但是superdirac有一点说得不错,就是对一个构型(即体系的一个微观状态),是无法计算自由能的,至少你没有办法对它定义熵项。有时候,比如我们对一个晶体,可以求它的自由能。
晶体是规则排布的,看上去我们似乎是对一个确定的构像来求自由能,实际上我们还是针对一个体系来求的,不管你是用MC、MD方法求统计平均,还是用计算声子之类的方法,都是考虑的整个体系而不是一个给定的构像,也就是考虑了体系的大量微观状态,或者说考虑了原子在平衡位置附近的振动。
所以我觉得,Yahoohoo在谈论自由能的时候,可能也无意中搞混了一些东西。 以上是我个人的一点感觉,还没有经过深思,大家还可以再来讨论,我说的有不对之处请多批评。