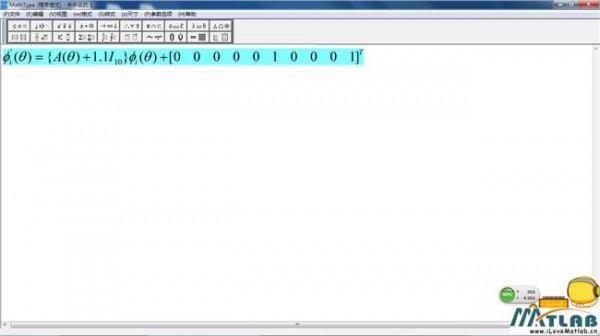
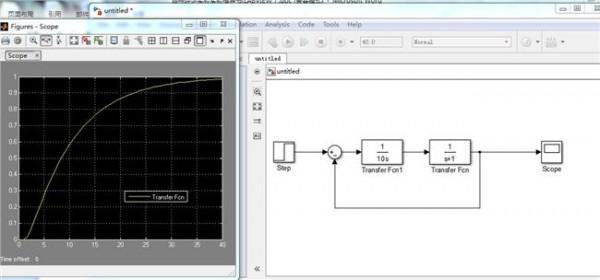
李雅普诺夫稳定性的李雅普诺夫稳定性理论
简介 俄国数学家和力学家A.M.李雅普诺夫在1892年所创立的用于分析系统稳定性的理论。对于控制系统,稳定性是需要研究的一个基本问题。在研究线性定常系统时,已有许多判据如代数稳定判据、奈奎斯特稳定判据等可用来判定系统的稳定性。
理论能同时适用于分析线性系统和非线性系统、定常系统和时变系统的稳定性,是更为一般的稳定性分析方法。理论主要指李雅普诺夫第二方法,又称李雅普诺夫直接法。李雅普诺夫第二方法可用于任意阶的系统,运用这一方法可以不必求解系统状态方程而直接判定稳定性。
对非线性系统和时变系统,状态方程的求解常常是很困难的,因此李雅普诺夫第二方法就显示出很大的优越性。与第二方法相对应的是李雅普诺夫第一方法,又称李雅普诺夫间接法,它是通过研究非线性系统的线性化状态方程的特征值的分布来判定系统稳定性的。
第一方法的影响远不及第二方法。在现代控制理论中,李雅普诺夫第二方法是研究稳定性的主要方法,既是研究控制系统理论问题的一种基本工具,又是分析具体控制系统稳定性的一种常用方法。
李雅普诺夫第二方法的局限性,是运用时需要有相当的经验和技巧,而且所给出的结论只是系统为稳定或不稳定的充分条件;但在用其他方法无效时,这.
..简介 俄国数学家和力学家A.M.李雅普诺夫在1892年所创立的用于分析系统稳定性的理论。对于控制系统,稳定性是需要研究的一个基本问题。在研究线性定常系统时,已有许多判据如代数稳定判据、奈奎斯特稳定判据等可用来判定系统的稳定性。
理论能同时适用于分析线性系统和非线性系统、定常系统和时变系统的稳定性,是更为一般的稳定性分析方法。理论主要指李雅普诺夫第二方法,又称李雅普诺夫直接法。李雅普诺夫第二方法可用于任意阶的系统,运用这一方法可以不必求解系统状态方程而直接判定稳定性。
对非线性系统和时变系统,状态方程的求解常常是很困难的,因此李雅普诺夫第二方法就显示出很大的优越性。与第二方法相对应的是李雅普诺夫第一方法,又称李雅普诺夫间接法,它是通过研究非线性系统的线性化状态方程的特征值的分布来判定系统稳定性的。
第一方法的影响远不及第二方法。在现代控制理论中,李雅普诺夫第二方法是研究稳定性的主要方法,既是研究控制系统理论问题的一种基本工具,又是分析具体控制系统稳定性的一种常用方法。
李雅普诺夫第二方法的局限性,是运用时需要有相当的经验和技巧,而且所给出的结论只是系统为稳定或不稳定的充分条件;但在用其他方法无效时,这种方法还能解决一些非线性系统的稳定性问题。
现在, 随着计算机技术的发展,借助数字计算机不仅可以找到所需要的李雅普诺夫函数,而且还能确定系统的稳定区域。 但是想要找到一套对于任何系统都普遍使用的方法仍很困难。 从上面的这段文字里可以看出,所谓任意函数指的是在一定范围的稳定区域内任选的,并不是所有函数都可以判断为系统稳定的。展开