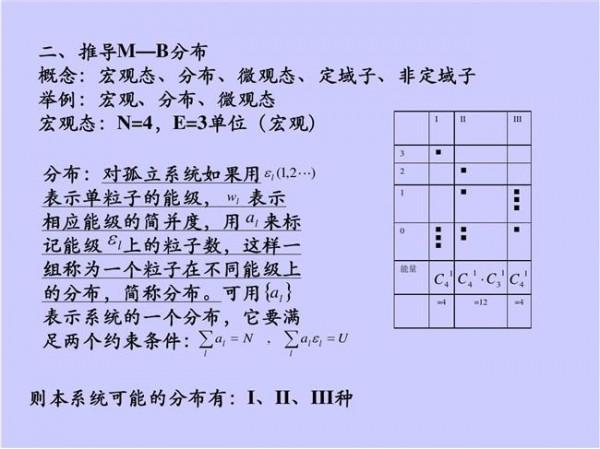
泰勒展开式意义 泰勒展开的多项式有什么意义?
不必深究,大概了解就行。 做科学研究时,通过一些输入值,会测得一些输出, 在坐标系中描点,连接后会得到一条曲线,这时需要找与这条曲线图像相近的一个函数来表示这条曲线。我们设这条曲线的未知函数是, 1.要求所给函数与曲线在那些测得数据的点处的函数值相等。
2.在相关点处切线相同。 3.3阶导数,4阶导数相同,显然阶数越高,近似度就越高。 总体而言就是这么得出一个多项式函数的。 这相当于我们希望两辆汽车在某一点处的位移相同,速度相同,加速度相同,.
..那么这两辆汽车在某一点处的运动就非常近似了。 这是一个方面,另一方面,一段距离,可以用这种方法相加得到(芝诺): 这是用多项式表达一个整数的例子; 再次,求曲线与坐标轴构成的面积,也会出现这种情况,比如墨卡托级数就是求函数与坐标轴围成的面积时得到的一个多项式函数近似等于 所以,无论是科学上近似模拟一条曲线,还是古人的猜想(芝诺),还是用古老的方法求曲边形面积,都会得到用多项式近似表达一个函数的结论。
这就是用多项式函数表达一个函数的思想发展过程。 若有兴趣,可以看看差商与牛顿插值。