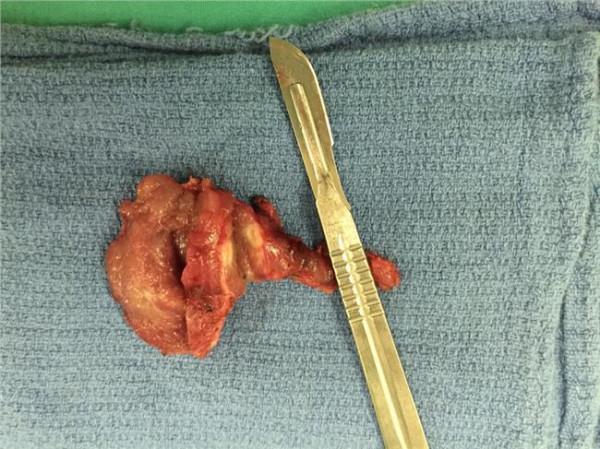
黄昆方程和非简谐振动

原因是前几节我们在求解原子运动方程时,只考虑了势能展开项中的二次项(简谐项),此时势能曲线是对称的,温度提高,原子振动幅度加大,并未改变其平衡位置,所以不会发生热膨胀。如果考虑到实际势能曲线的非对称性所带来的非简谐项的影响,上面的与实际晶体性质不相符的推论就都不存在了。

然而非谐项的存在将会给运动方程的求解带来很多的困难,所以我们在讨论非简谐效应时,往往更多的采用定性分析的方法,采用对简谐近似结论修订和补充的方法来适应非简谐的情况。

简谐近似,势能为抛物线,两边对称。Morse给出了双原子分子的势函数的一种表达式:见PeterBrueschPhonons:TheoryandExperimentsⅠP154对实际晶体而言,它们反抗把体积压缩到小于平衡值的能力要大于反抗把体积膨胀时的能力,所以势能曲线是不对称的,振幅增大,原子距离增大,这是发生热膨胀的根源。

Morse势能表达式,我们以此为例讨论非简谐效应:是离解能,是一个正值常数。

D从势能展开项开始讨论:常数定义为零平衡点微商为零简谐项非谐项…都是力常数,可以通过Morse函数的展开式给出。要注意不同书中系数的定义有所不同,并不影响讨论结果。证明见习题2.

11我们先只取到三次方项:简谐项非简谐项按照Boltzman统计,处于热平衡时,对平衡态的偏离:显然,不考虑三次方项,不会发生热膨胀。考虑了三次项后即可以解释热膨胀,此时线膨胀系数是常数:如果考虑比三次方以上的更高次项,膨胀系数就不再是线性的。

实验曲线表明了这点。(求解比较繁琐,需要假定:)=常数见Kittelp89先看一个双原子运动方程:是两原子的约化质量其解的形式为:这里只考虑了Fourier展开式中的头三项,所以只有2ω项,如果考虑项,则会有3ω的项。

②①③将③式代入①求解,并假定sA<<1,有:二.非简谐下的解:⑤利用③式,并考虑到:有:因为,所以:注意到势能曲线的斜率:即作用力下降,频率降低,见式④⑥⑤⑦当系统与热源处于热平衡状态时,双原子的平均振动能:代入⑦式可得:⑤式可以写成:从这个结果中我们得到启发:描述多原子分子的非简谐运动要复杂的多,不仅要有几个基本频率:还需要包括振幅平方与温度成正比≈考虑非简谐项后一维单原子链运动方程的求解:方程求解非常复杂,特别是非谐项比较大时,完全不能用类似的方法来表述,但我们在处理弱非简谐情况时,可以把简谐近似下得到的相互独立的简谐振子解作为基础,把非简谐项作为微扰来处理,这就导致声子之间存在着相互作用,会发生碰撞,能量改变且只有有限的寿命。

一种频率的声子可以湮灭而产生另一种频率的声子,这样经过一段时间后,各种频率的声子数目就会达到和环境温度相平衡的分布。

简单说就是通过非谐项的作用,本来相互独立的谐振子之间发生耦合,即两个声子之间可以发生碰撞而产生第三个声子,或说一个波矢为q1的声子,吸收一个波矢为q2的声子,变成一个波矢为q3的声子。

声子之间的碰撞要服从能量和动量守恒:Normalprocess正常过程Umklappprocess倒逆过程由于波数必须在第一布里渊区内取值,因此动量守恒的要求会存在两种情况:仍在第一布里渊区内的称正常过程;新声子的q值等于第一布里渊区内某个值加一个倒易矢量的称倒逆过程。

从下面图中可以清楚的看出倒逆过程是影响声子传播、降低热传导的主要因素。这里,波矢和波矢是对同一声子的,表述了同样一个运动状态。

正常过程NormalProcesses倒逆过程UmklappProcesses二维正方晶格中正常声子碰撞过程k1 k2=k3二维正方晶格中倒逆声子碰撞过程k1 k2=k3 Gl可以把倒逆过程看成是:一个声子被布喇格反射、同时伴随着吸收或发射另一个声子。

在任一声子碰撞过程中,没有什么进入或离开晶体,总动量是守恒的,我们认为动量和声子有关只是对晶体总动量的一种人为分割,是为了方便讨论问题而引入的。

一个声子的晶体动量并不是唯一确定的,和是同一个声子。唯一在物理上可以定义的量是一个声子波包所携带的动量,当振动完全简谐时,此动量为零。所以:晶体动量和真实动量实际上是两个极不相同的概念,上面的等式应看作是关于波矢的几何干涉条件,而不视为动量守恒定律,才是更为正确的概念。

三.绝缘体的热导率当固体中的温度不均匀时,将会有热能从高温处流向低温处,这种现象称作热传导。实验表明:单位时间内通过单位面积的热能(称作热流密度)与温度梯度成正比,其比例系数称作热导率。

在简单假定温度T只是x方向的函数时,有:负号表示热能传输总是从高温到低温。固体中,可以通过自由电子传热,也可以通过格波来传热,本节只讨论绝缘体的热导,即晶格热导:热能以格波群速度在固体中传播。

简谐近似下无杂质、无缺陷的晶体其热导率应该趋于无穷,这与事实不符,在考虑了格波与晶体边界、杂质原子、缺陷及格波之间的相互作用后,绝