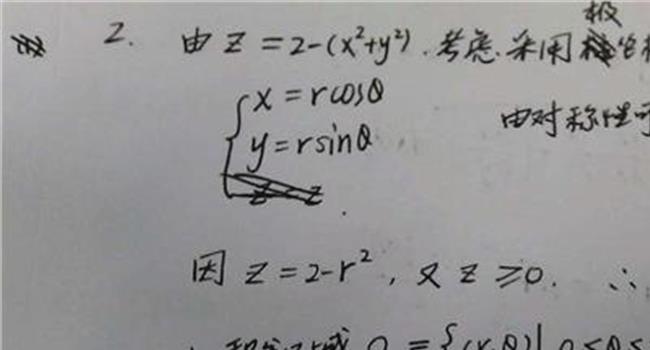【微积分基础知识】有关微积分理论的学习和体会

读过大学特别是理工科院校或数学专业的人都不会忘记在校微积分的学习过程,学后多年不用能否很清楚的还掌握和灵活运用,确实是个问题,本文就是要帮助那些还没学懂的少部分朋友们,重温微积分的原理和有关关联联系问题。

很好掌握已学的知识问题。人类为何要发明微积分?是为了解决什么问题?一切科技成果的产生是源于当时的社会生产需要,以及环境的促进有关,由于生产的发展,机械制造、建筑、航海、军事武器等实业的发展,许多生产现实问题摆在工程技术、及研究者面前,如:变速运动、不规则图形面积等这些问题是初等数学那已解决的,因而数学从研究常量为主初等数学,发展到以研究反映客观事物运动变化过程的变量为主的高等数学,微积分是高等数学的一个主要组成部分,从初等数学发展到高等数学,是数学史上一个飞跃,恩格斯曾经指出过:数学中的转折点是笛卡尔的变数(函数),有了变数运动进入了数学,有了变数,辩证法进入了数学,函数概念和理论后微积分学术思想初露头角,是继尤拉几何之后,是数学理论中一个最大的创造。

微积分的创立。首先是为了处理和解决十七世纪科技前沿有关科技难题:1.不断变化的即时速度和加速度问题。2.物理光学引出的变化的曲线和切线问题。3.求函数的最大值与最小值问题。4.求曲线长度等问题.。

促使微积分产生的因素:是函数概念的采用,即用符号阐明事物要素的关联关系这是科学的再发展的铺垫:v=RT/P, 是表明一定量的理想气体在体积V是它的压强P和它的绝对温度的函数。Q=UIt, 表明电力用户所耗电能Q是电压U,电流I和时间它的函数,引入U=IR欧姆定律便得Q=R(I^2) t , s=r 这就是机械上曲柄滑块机构中滑块位置和曲柄转角之间的函数关系。

微积分是顺应军事和生产中的相关数学的发展,经过很多数学家研究成果积累并总结起来的一套数学运算系统,目的是为了解决各种科学模型中的变量求解问题。微积分作为初等数学和高等数学的分水岭,在现代科学中有着极其重要的作用,微积分的发明也绝对堪称人类智慧的结晶。

在17世纪以前,很多数学家已经开始萌发了微积分的思想;比如中国古代数学家祖冲之利用割圆术求圆周率,阿基米德的微元法求体积、希腊数学家的极限思想等等。科学是人们的社会实践(物质生产、国防安全、科学实验、等等)的产物和工具,因需要促引发展。

数学中的微积分学问的发生与发展主要也是这样,古代生产水平底下需要和涉及的数学和其它科学就简单;近代生产的逐渐发达,科学技术在进步,数学和其它科学一样,也日趋复杂。随着社会生产实践发展到一定阶段,常量的数学就不够用了,于是变量的数学应运而生处理和解决变化现象的重要数学学科。

微积分学科由十七世纪的英国人牛顿与德国人莱布尼兹同时独立发现。微积分是微分法与积分法的简称。微分法和积分法是对立统一的两种分析和计算方法犹如加法和减法、乘法和除法。

微分是将研究的对象虚拟划分为极其细微的小部分,这种极其微小部分被称为无穷小量,有大变小,由小变为无穷小,目的是要实现计算方式上的转变,以直代去曲,以不变代可变,以微小直至极限理论去分析化解计算整体和部分变量数学的转变性分析数学的科学。

正如恩格斯指出的:“只有微分学才能使自然科学有可能用数学不仅仅表明状态,并且也表明过程:运动。”

人们对几何图形的认识过程,同认识其它事物一样,也是经历了从简单到复杂、从直观到抽象的过程。在初等数学中直线和曲线是两个不同性质的感念,直线和曲线很明显有着不同的外观和几何特征。但是直曲线能不能在一定条件下实现转化呢?可以转化的,古代劳动人民在他们生产实践中已经实现了直和曲的转化了,他们用条形或方形直砖砌成成拱形的桥,如赵州桥等历史古迹。

另外,我国魏晋时期的刘徽和南北朝时期的祖冲之利用圆的内正多边形去计算圆的周长和面积也是利用直线和曲线的转化达到目的的。

到了十七世纪以后,随着数学微积分理论的产生和发展人们对直和曲的关系的认识计入了一个新阶段。当时恩格斯曾指出:高等数学的主要基础之一是这样一个矛盾:在一定条件下直线和曲线应当是一回事。

认识和认知来源与概念,什么是概念?概念是反映事物本质属性的思维表达形式。内涵是概念的质的体现,外延是概念量的表达,通常是指本概念使用范围。

从事物及要素间的关联看,从数学角度来分析有的是始终保持不变的量被成为常量或常数,有的是可以变化的量被成为变量或变数。事物要素间的关联体现在一个要素的变化或改变,会引起相关联的两个要素的变化或改变,这种要素间的关联关系被称为函数关系。

函数的导数是指函数因变量的变化率与自变量的变化率之比,也称微商;导数的通俗定义:在函数某一定义域内,自变量有微小改变引起因变量的的改变值与自变量改变中商值的极限

函数差商的极限称为函数y=f(x)在点x处的导数。 函数的差商{f() - f(x)}/

(-x) = y-y /x-x =△y /△x 来源于:微积分和数学分析引论 R.克朗 F 约翰 著

西安交大高等数学中导数的定义:设有函数y=f(x),当自变量x在处有改变量△x时,函数y相应地有改变量△y=f( △x)-f();如果这两个该变量之比当 0时的极限。存在,那么这极限值称为函数y=f(x)在的导数。并说函数f(x)在可导,记作 f'()或 y'

1.判断该区域段函数的升、降、以及升降快慢,2.求函数在改点最大值(极值)3.求解事物要素间关联关系:1)运动的速度是路程对于时间的导数,即v=ds/dt.,2)比热是热量对于温度的导数,即c=dq/dτ,3)线性密度是质量对于长度的导数,即δ=dm/ 。

一种理论的诞生是社会生产需要所促进的产物,学习理论目的是要能掌握事物要素间关联关系,能更清楚的认识事物和认知事物,学习的目的全在于应用,在应用中获取效益和成果。

导数是一个数学概念。微积分和数学分析引论(R.柯朗.F.约翰 著)函数差商的极限称为函数y=f(x),在x点处的导数,是计算和分析力学中的瞬时速度、电学中的电流强度、化学中的反应速度等有力工具。1.可对函数线性化处理和分析计算。2.应用生产和测量及工厂技术中的近似计算公式的推导计算。3.可分析曲线的凹凸性判断函数变化趋势。4.求函数的极值(最大最小值)

微分的定义:函数y=f(x)在x点可导,则f'(x)dx,称为函数y=(x)在x点的微分。通俗来讲:函数在某曲线上的一点可导,函数自变量的改变量与其在该点导数之积成为给函数在该点的微分。

在微分的定义中可知,dy和dx是同时存在的,它们的比:就是导数f'(x),所以导数也叫微商。

早在希腊时期,人类已经开始讨论「无穷」、「极限」以及「无穷分割」等概念。这些都是微分的中心思想;虽然这些讨论从现代的观点看有很多漏洞,有时现代人甚至觉得这些讨论的论证和结论都很荒谬,但无可否认,这些讨论是人类发展微分的第一步 。

例如公元前五世纪,希腊的德谟克利特(Democritus)提出原子论:他认为宇宙万物是由极细的原子构成。在中国,《庄子.天下篇》中所言的「一尺之捶,日取其半,万世不竭」,亦指零是无穷小量。这些都是最早期人类对无穷、极限等概念的原始的描述。

其他关于无穷、极限的论述,还包括芝诺(Zeno)几个著名的悖论:其中一个悖论说一个人永远都追不上一只乌龟,因为当那人追到乌龟的出发点时,乌龟已经向前爬行了一小段路,当他再追完这一小段,乌龟又已经再向前爬行了一小段路。

芝诺说这样一追一赶的永远重覆下去,任何人都总追不上一只最慢的乌龟--当然,从现代的观点看,芝诺说的实在荒谬不过;他混淆了「无限」和「无限可分」的概念。人追乌龟经过的那段路纵然无限可分,其长度却是有限的;所以人仍然可以以有限的时间,走完这一段路。然而这些荒谬的论述,开启了人类对无穷、极限等概念的探讨,对后世发展微积分有深远的历史意味。

另外值得一提的是,希腊时代的阿基米德(Archimedes)已经懂得用无穷分割的方法正确地计算一些面积,这跟现代积分的观念已经很相似。由此可见,在历史上,积分观念的形成比微分还要早--这跟课程上往往先讨论微分再讨论积分刚刚相反。

十七世纪的大发展牛顿和莱布尼茨的贡献

中世纪时期,欧洲科学发展停滞不前,人类对无穷、极限和积分等观念的想法都没有什么突破。中世纪以后在微分方面,十七世纪人类也有很大的突破。费马(Fermat)在一封给罗贝瓦(Roberval)的信中,提及计算函数的极大值和极小值的步骤,而这实际上已相当于现代微分学中所用,设函数导数为零,然后求出函数极点的方法。

另外,巴罗(Barrow)亦已经懂得透过「微分三角形」(相当于以dx、dy、ds为边的三角形)求出切线的方程,这和现今微分学中用导数求切线的方法是一样的。

由此可见,人类在十七世纪已经掌握了微分的要领。微分概念是在解决直与曲的矛盾中产生的,在微小局部可以用直线去近似替代曲线,它的直接应用就是函数的线性化。微分具有双重意义:它表示一个微小的量,因此就可以把线性函数的数值计算结果作为本来函数的数值近似值,这就是运用微分方法进行近似计算的基本思想

微分概念是在解决直与曲的矛盾中产生的,在微小局部可以用直线去近似替代曲线,它的直接应用就是函数的线性化。微分具有双重意义:它表示一个微小的量,因此就可以把线性函数的数值计算结果作为本来函数的数值近似值,这就是运用微分方法进行近似计算的基本思想,是在无限微小分化的极限条件原理情况下实现由曲到直的转变的一种数学分析和数学上的手段和工具。

从直到曲,由曲化直的认识是先由形的客观事物为上学的认识开始的,在欧几里几何学中人们开始认识形,研究直线和圆的某些性质,面对复杂的曲线图形还很少研究。人类在认识史上先认识事物,而后才能研究过程。必须先知道一个事物是什么,而后才能觉察这个事物中所发生的变化。

导数是函数图像在某一点处的斜率,也就是纵坐标增量(Δy)和横坐标增量(Δx)在Δx0时的比值的极限。微分是指函数图像在某一点处的切线在横坐标取得增量Δx以后,纵坐标取得的增量,一般表示为dy。导数是函数图像在某一点处的斜率,也就是纵坐标变化率和横坐标变化率的比值。微分是指函数图像在某一点处的切线在横坐标取得Δx以后,纵坐标取得的增量。

微分在数学中的定义:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。微积分的基本概念之一。

微分定义:设函数y = f(x)在x的邻域内有定义,x及x Δx在此区间内。如果函数的增量Δy = f(x Δx) - f(x)可表示为 Δy = AΔx o(Δx)(其中A是不依赖于Δx的常数),而o(Δx)是比Δx高阶的无穷小(注:o读作奥密克戎,希腊字母)那么称函数f(x)在点x是可微的,且AΔx称作函数在点x相应于因变量增量Δy的微分,记作dy,即dy = AΔx。

函数的微分是函数增量的主要部分,且是Δx的线性函数,故说函数的微分是函数增量的线性主部(△x→0)。

导数与函数的区别之处:导数和微分的区别一个是比值的极限、一个是增量。

1、导数是函数图像在某一点处的斜率,也就是纵坐标增量(Δy)和横坐标增量(Δx)在Δx-->0时的比值。

2、微分是指函数图像在某一点处的切线在横坐标取得增量Δx以后,纵坐标取得的增量,一般表示为dy。

函数的导数等于函数的微分与自变量的微分之商。也就是微分之值既自变量x有关,也与dx有关。

微分应用:

1、我们知道,曲线上一点的法线和那一点的切线互相垂直,微分可以求出切线的斜率,自然也可以求出法线的斜率。

2、假设函数y=f(x)的图象为曲线,且曲线上有一点(x1,y1),那么根据切线斜率的求法,就可以得出该点切线的斜率m:m=dy/dx在(x1,y1)的值,所以该切线的方程式为:y-y1=m(x-x1)。由于法线与切线互相垂直,法线的斜率为-1/m且它的方程式为:y-y1=(-1/m)(x-x1)

3、增函数与减函数

微分是一个鉴别函数(在指定定义域内)为增函数或减函数的有效方法。

鉴别方法:dy/dx与0进行比较,dy/dx大于0时,说明dx增加为正值时,dy增加为正值,所以函数为增函数;dy/dx小于0时,说明dx增加为正值时,dy增加为负值,所以函数为减函数。

4、变化的速率

微分在日常生活中的应用,就是求出非线性变化中某一时间点特定指标的变化。

在t=3时,我们想知道此时水加入的速率,于是我们算出dV/dt=2/(t 1)^2,代入t=3后得出dV/dt=1/8。

所以我们可以得出在加水开始3秒时,水箱里的水的体积以每秒1/8升的速率增加。

随着物理学方面的发展,很多物理问题的研究遇到了困难,比如:行星椭圆轨道的推导过程、最速降曲线问题、 曲线的切线问题、函数极值问题、复杂球体的体积问题等等。这时候科学家们对以上问题的解决,有着非常迫切的需求,期间很多数学家对微积分的诞生做了铺垫,比如笛卡尔发明坐标系、费马、开普勒、伽利略、哈雷等人也有贡献。

最终在17世纪末,英国数学家牛顿和德国数学家莱布尼兹,分别独立地发明了微积分,两者对微积分的切入点不一样,但是本质思想是一致的。微积分的诞生,对以上科学问题,简直犹如天助,轻轻松松就能解决很多以前解决不了的问题;虽然微积分在创立之初遭遇到很多难题,但都被后来的数学家们完善。

微积分的基本思想是求极限,函数角度看就是求切线和面积,又可分为积分和微分两大类,两者互为逆运算。

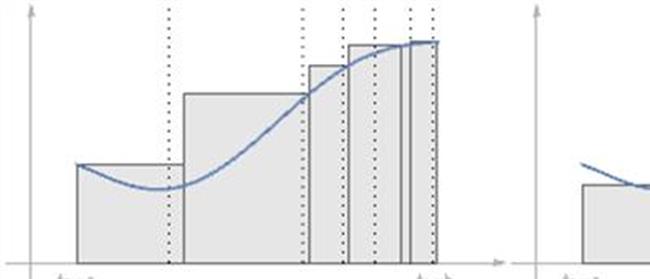
比如下图:对于一个函数f(x),在定义域[a,b]内,函数图像和横坐标围成一个阴影面积,如果要求阴影面积的大小,只用初等数学知识是很难的,但使用微积分就变得非常简单。

微积分有一套严格的微分和积分法则,比如该函数表达式为f(x)=x^3,a=2,b=5,那么可以很快求出阴影部分的面积:

微积分的发明与发展离不开实际需要,在16、17世纪科学技术处于攻坚阶段,当时的物理学家牛顿在研究力学,流体力学的问题中,提出了很多新课题,这些问题使用当时的数学方法是无法解决的,于是牛顿和莱布尼兹发明了微积分理论。

最早,伽利略在研究力学时,提出了变量的概念,这是函数的基础,在他的著作里提出全新的数学概念,后来经过数学家莱布尼兹的发展,引进了函数符号的概念,这样就给微积分的诞生打下了坚实的基础。

而牛顿发明微积分几乎是和牛顿平行而独立进行的,他们俩对函数的称呼也不一样,一个叫做function,沿用至今,另一个叫做fluent,即:流量,为什么牛顿把它叫做流量呢?因为当时他在研究流体力学。

当时的科技发展给数学家门出了几个难题,比如如何在已知位移公式的情况下求出v、a(速度、加速度),又如已知曲线方程求其某个点上的切线,或者求出曲线某段的弦长,还有在某个区间内,求出函数的最大或者最小值问题。

牛顿在解决这些问题时,使用到了极限的运算,后来就出现了对函数的求导数运算,这样就发明了微分学,有了微分学理论,就可以解决上面提到的求物体运动的瞬间速度和加速度问题,就可以求出曲线在某点的切线问题。

后来,这些物理力学家和数学家发现光有微分理论,还不能解决其他问题,比如已知速度公式如何求出位移函数,已知曲线函数如何求出在某个区间上内围成图形的面积,以及如何求曲线的长度等。

这些问题的解决,同样离不开极限运算,在物理学家和数学家们的辛勤劳动下,积分学终于诞生了。在微积分学的发展历程中,牛顿和莱布尼茨是代表性的人物,他们做出了巨大贡献,微积分的发展是科学技术发展的重要的里程碑。是定量数学向变量数学转变的一个阶梯。