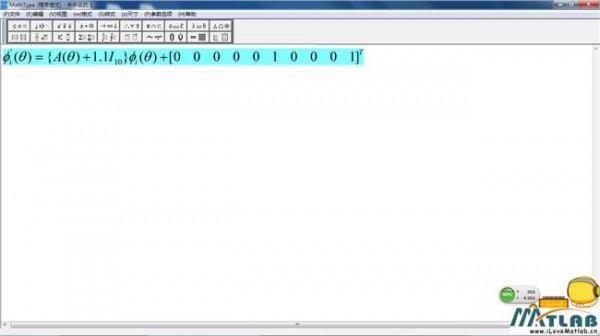
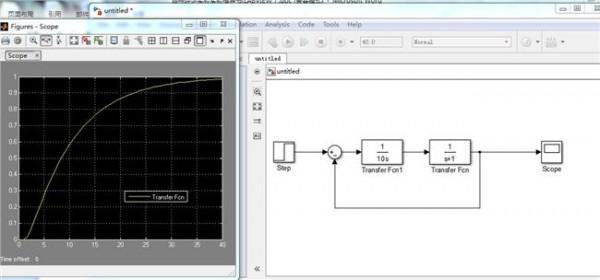
李雅普诺夫稳定理论的定义及应用
控制系统计算机辅助设计---MATLAB语言与应用第四章稳定性 与李雅普诺夫方法稳定性是一个控制系统工作的首要、必要条件。经典控制理论判稳方法:劳斯判据、根轨迹法、奈氏判据、对数频率判据.适用范围:线性定常系统,不适用于非线性和时变系统。
描述函数法:要求系统线性部分具有良好的滤波性能。相平面法:只适合于一阶、二阶非线性系统。早在1892年,俄国学者李雅普诺夫(AleksandrMikhailovichLyapunov,1857–1918)发表题为“运动稳定性一般问题”的著名文献,建立了关于运动稳定性研究的一般理论。
1892年俄国学者李雅普诺夫(Lyapunov)提出的稳定性理论,给出了两种判别方法:Lyapunov第一法和Lyapunov第二法不仅适用于单变量线性系统,还适用于多变量、非线性、时变系统,它是确定系统稳定性的更一般理论;Lyapunov第一法:通过求解系统微分方程,根据解的性质来判断系统的稳定性;Lyapunov第二法:不用求解方程,通过Lyapunov函数来判断系统的稳定性。
补充知识4.1李雅普诺夫关于稳定性的定义4.1李雅普诺夫关于稳定性的定义4.2李雅普诺夫第一法Lyapunov第一法又称间接法。
它的基本思路是通过系统状态方程的解来判断系统的稳定性。对于线性定常系统,只需解出特征方程的根就可以作出稳定性判断。对于非线性不是很严重的系统,则可以通过线性化处理,得到近似线性方程,然后再来判断。
4.2李雅普诺夫第一法定义:若所有有界输入引起的零状态响应输出有界,则称系统为有界输入输出稳定。(BIBO)注:1.由于传递函数阵中出现了零极点对消的情况:2.只有当系统的传递函数不出现零极点相消现象,并且矩阵A的特征值和传递函数的极点相同时,内部稳定才和BIBO稳定一致。
4.2李雅普诺夫第一法4.3Lyapunov第二法李氏第二法称为直接法,建立在用能量观点分析稳定性的基础上。
若系统的平衡状态是渐近稳定,则系统激励后其存储的能量将随着时间的推移而衰减;当趋于平衡状态时,其能量达到最小值;反之,若系统的平衡状态是不稳定的,则系统将不断从外界吸收能量,其存储的能量将越来越大。
4.3Lyapunov第二法4.3Lyapunov第二法`李雅普诺夫(Lyapunov)函数例1试确定用如下状态方程描述的系统的平衡态稳定性。4.3Lyapunov第二法注:恒等于零,这时的运动轨迹将落在某个特定的曲面上。
这就意味着运动轨迹不会收敛于原点。这种情况对应于非线性系统中的极限环或是线性系统中的临界稳定。不恒等于零,这时的运动轨迹只在某个时刻与某个特定的曲面相切,运动轨迹通过切点后并不停留而继续向原点收敛。
这种情况仍然属于渐近稳定。4.3Lyapunov第二法4.3Lyapunov第二法由上节知,李雅普诺夫第二法是分析动态系统的稳定性的有效方法,但具体运用时将涉及到如何选取适宜的李雅普诺夫函数来分析系统的稳定性。
由于各类系统的复杂性,在应用李雅普诺夫第二法时,难于建立统一的定义李雅普诺夫函数的方法。目前的处理方法是,针对系统的不同分类和特性,分别寻找建立李雅普诺夫函数的方法。
设线性定常连续系统的状态方程为这样的线性系统具有如下特点:当系统矩阵A为非奇异时,系统有且仅有一个平衡态xe=0,即为状态空间原点;若该系统在平衡态xe=0的某个邻域上是渐近稳定的,则一定是大范围渐近稳定的;对于该线性系统,其李雅普诺夫函数一定可以选取为二次型函数的形式。
4.4李雅普诺夫方法在线性系统中的应用证明(1)先证充分性。即证明,若对任意的正定矩阵Q,存在正定矩阵P满足方程ATP PA=-Q则平衡态xe=0是渐近稳定的。
证明思路:(2)再证必要性。即证明:若系统在xe=0处是渐近稳定的,则对任意给定的正定矩阵Q,必存在正定矩阵P满足矩阵方程:PA ATP=-Q证明思路:由正定矩阵Q构造满足矩阵方程PA ATP=-Q的正定矩阵P。
证明过程为:对任意给定的正定矩阵Q,构造矩阵P如下在应用上述基本定理和推论时,还应注意下面几点:(1)如果V’(x,t)=-xTQx沿任意一条状态轨线不恒为零,那么Q可取为非负定矩阵,而系统在原点渐近稳定的充要条件为:存在正定矩阵P满足李雅普诺夫代数方程(3)运用此方法判定系统的渐近稳定性时,最方便的是选取Q为单位矩阵,即Q=I。
于是,矩阵P的元素可按如下李雅普诺夫代数方程:PA ATP=-I求解,然后根据P的正定性来判定系统的渐近稳定性。
不难看出,原点为系统的平衡状态。选取Q为非负定实对称矩阵,则Matlab判断系统的李雅普诺夫稳定性。基于矩阵特征值判定李雅普诺夫方程的解的正定性,再来判定线性系统的渐近稳定性。
4.4李雅普诺夫方法在线性系统中的应用2线性时变连续系统的稳定性分析证明1)先证充分性。即证:若对任意的正定矩阵Q(t),存在正定矩