【秦九韶的高次方程解法】秦九韶的高次方程
公元1819 年7 月1 日,英国人霍纳在皇家学会宣读了一篇数学论文,提出了一种解任意高次方程的巧妙方法,一时引起了英国数学界的轰动。
由于这一方法有其独到之处,而且对数学科学有很大的推进作用,因而这一方法被命名为“霍纳方法”。但是没过多久,意大利数学界就提出了异议,因为他们发现自己的同胞鲁菲尼已在15 年前就得到了同样的方法,只是没有及时地报道罢了。

因此,意大利数学界要求将这一数学方法命名为“鲁菲尼方法”。于是英、意双方开始了喋喋不休的争论。正巧,有个阿拉伯人前往欧洲,听到了双方的争论后,不置可否地大笑起来。争论双方问他,为何这般嘲笑。

这位阿拉伯人从背包中掏出一本书,递与争论双方,说道:“你们都不要争了,依我看来,这个方法应该称作‘秦九韶方法’”。他们这才知道,早在570 多年前,有个叫秦九韶的中国人就发明了这种方法。双方觉得他们的这场争论已显得毫无意义了。

秦九韶,生于1202 年,南宋普州安岳(今四川安岳)人。他自幼随做官的父亲周游过许多地方。20 岁的时候,秦九韶随父亲来到南宋的都城——临安(今杭州)。秦九韶被父亲送到掌管天文历法的大史院学习。在这里,他了解了制定历法的一些基本算法和理论依据,这对于他后来写作著名的《数书九章》大有益处。

后来他回到四川老家,在一个县城里当县尉,这时,北方的元兵大举进犯,战乱频繁。他在这种动乱的环境中度过他的壮年。后来他在《数书九章》中写了“天时”和“军旅”等问题,想必与这段生活有关。
过了几年,秦九韶的母亲去世了,他按照封建社会的传统,回家为母亲守孝三年。正是在这段时间里,秦九韶完成了他的辉煌的数学著作——《数书九章》。
《数书九章》共分九大类,每类各有九题,全书共有81 道数学题目,内容包括天时、军旅、赋役、钱谷、市易等类问题。在这81 道题目中,有的题目比较复杂,但题后大多附有算式和解法。正是在这些解法中包含着许多杰出的数学创造,高次方程的解法就是其中最重要的一项。
高次方程就是未知数的最高次幂在3 次以上的。对于一元二次方程,我们可以用求根公式来解,三、四次的求根公式很复杂,至于五次以上的方程,那就没有求根公式。那么用什么办法来解决呢?秦九韶创造的这种解法是一种近似的解法,但是它能够把结果算到任意精确的程度,只要你按照一些简单的程序,反复地进行四则运算即可。除了高次幂方程的解法之外,这本书中的另一项伟大成就是关于同余式方面的工作。什么叫同余式呢?
我们还是从“韩信点兵”的故事来说起:
什么叫同余式呢?在上面的故事中,如果三人一组剩2 人,那么总人数可能是5、是8、也可能是11⋯⋯。换句话说,5、8、11⋯⋯这些数被3 除后余数相等,那么我们就说5、8、11⋯⋯等数对于3 是同余的,用数学符号写出来就是5≡8≡11(mod3),这个式子叫同余式。
秦九韶在写作《数书九章》时,把当年在太史局学到的天文学知识与《孙子算经》的数学问题结合起来,发展了同余式的理论和算法,从而圆满解决了韩信点兵之类问题。
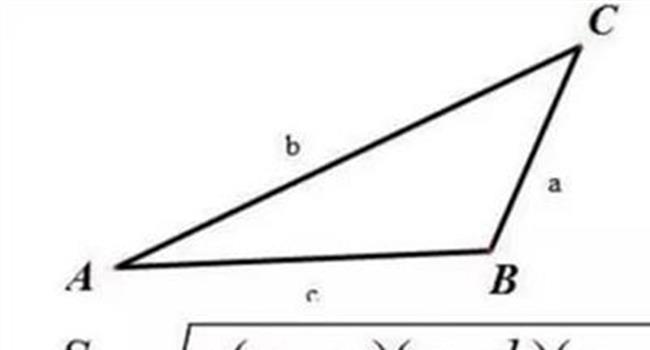
秦九韶还有许多数学创造,他是世界上最早提出十进小数概念和表示法的人。他还独立地推导出已知三边求三角形面积的公式:
秦九韶在多元一次方程组和几何测量方面也有创新。他是世界上最伟大数学家之一,《数书九章》标志着中国的古代数学达到了一个新的高峰。