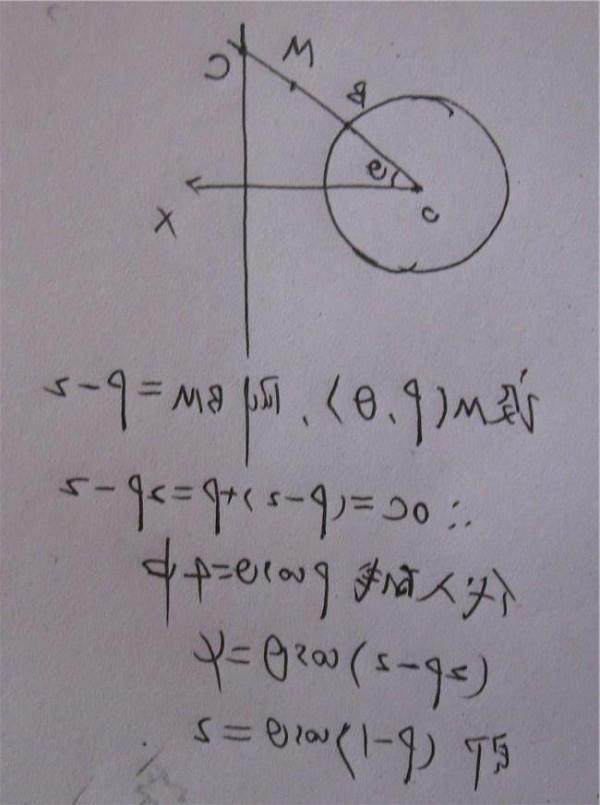【笛卡尔坐标系】关于笛卡尔坐标系与点和矢量
二维笛卡尔坐标系包含两个信息 1.一个特殊的位置,即坐标系的中心——原点。 2.两条过原点相互垂直的矢量,级x轴与y轴。
在三维笛卡尔坐标系中我们需要定义三个坐标轴和一个原点,这个三个坐标轴称之为基矢量,他们相互垂直,且长度为1,这样的基矢量被称为标准正交基。

在Unity中我们所使用的三维笛卡尔坐标系是基于左手坐标系的。为什么三维分有左右手之分呢?在二维坐标中我们可以通过一些旋转操作使OpenGL和DirectX的坐标轴只想相同,但对于三维笛卡尔坐标系来说,靠这种旋转有时并不能让两个不同朝向的坐标系重合。他们之间并没有优劣之分,无论使用那种坐标系绝大多数情况下是不会影响底层数学运算的。

但对于观察空间来说,Unity使用的是右手坐标系。
点是维度空间里的一个位置,在笛卡尔坐标系中我们使用两三个实数来表示一个坐标,如P=(Px,Py)表示二维空间点,P=(Px,Py,Pz)表示三维空间点。 矢量(也称为向量)指包含了模和方向的带方向线段。

单位矢量指那些模为1的矢量。
注意:矢量不可以和一个标量相加或相减,或者和不同维度的矢量进行运算。
1.公式一
如果我们用一个单位矢量A和另一个长度不限的矢量b点乘,那么我们就会得到b在A方向上的投影(通俗来讲就是垂直于A的光源,照射b得到的影子称为投影,如图)。

2.公式二
至于为什么会得到这个公式,我们先继续看图,首先一个矢量我们可以拆分为单位向量和它的模,由此我们可以推导出公式的前面两部分。假设矢量A和矢量B的模都为1,也就是他们两的单位矢量相点乘,得到的投影也就是下图红色部分。
还记得三角函数中的(余弦cosθ=直角边/斜边)公式吧,从图中我们不难看出两个单位向量相乘刚好得到它们夹角余弦所对应的直角边,因此我们反推可以得到下面的公式。
也就是说,两个矢量点积可以表示为两个矢量的模相乘,再乘以它们之间夹角的余弦值。 通过这个公式我们还可以求出两个想浪之间的夹角(0°~180°之间)。这里arcos是反余弦操作。
叉积不满足交换律,aXb不等于bXa,但是aXb=-(aXb)。
这个公式我们用一个平行四方形来推导。我们知道平行四边形的面积=底X高,可以使用
b
乘以h来得到,而h又可以用
a
和夹角sinθ正弦得到。
所以,推导出如下公式
注意:如果两个向量平行,那么我们所得到的面积为0,这里的是0向量,而不是标量0. 叉积的作用:通过叉积我们可以得到垂直于两个矢量平面的一个新的矢量,根据这个矢量的正负值我们可以判断该平面的朝向。(例如:V(6,4,-3),这里我们可以知道该矢量的Z轴朝向是负方向的。)