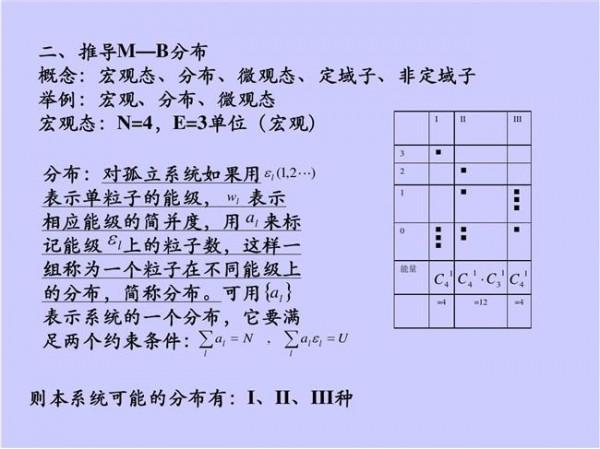
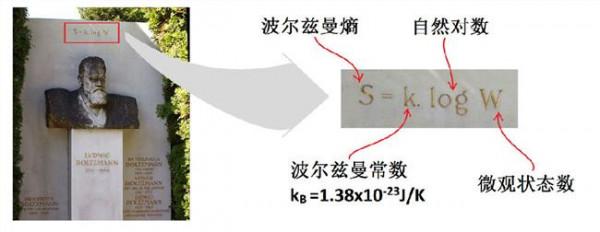
玻尔兹曼分布的严格推导
【摘要】:在运用较高精度的斯特林公式基础上,利用拉格朗日不定乘子法,结合带拉格朗日余项的n元泰勒展开式,以兰伯特W函数的形式,给出了精度更高的一种玻尔兹曼最概然分布及其严格的理论推导,并附带给出较低精度的斯特林公式下的推导结果.此方法可以很容易推广到玻色分布和费米分布中去.
【作者单位】: 东南大学吴健雄学院;东南大学物理系; 【关键词】: 玻尔兹曼分布 拉格朗日不定乘子法 斯特林公式 n元泰勒展开式 兰伯特W函数 【分类号】:O552.3-4;G642 【正文快照】: 在统计物理中,对于玻尔兹曼最概然分布,通常都是使用拉格朗日乘子法,推导出需要的分布形式.
但是一般教科书[1,2]为了保留直观的物理图像而舍弃了推导过程中的严密性.例如在处理二阶导数时,和n元函数微分学的基本理论[3-5]存在出入,使得玻尔兹曼最概然分布的“最概然”3个字略